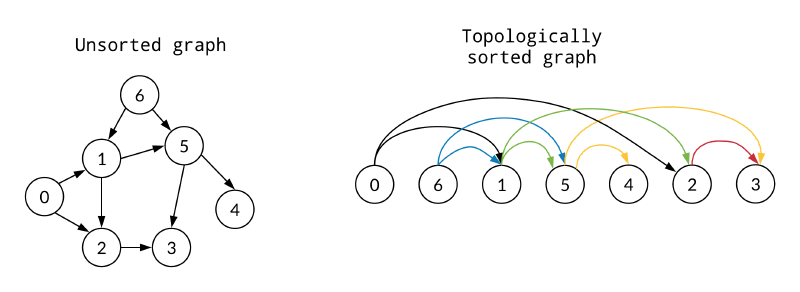
拓扑排序(Topological Sorting)是图论中一个比较重要的概念。它主要用来解决下面这类问题:
给定一个 AOV 网(Activity On Vertex Network), $ A\rightarrow B $ 表示活动 $ A $ 必须在活动 $ B $ 之前完成。请给出一个合理的活动顺序。
当然,AOV 网中不可能出现环,因为出现了环就无法拓扑排序。因此可以用拓扑排序来判断图中是否存在环。
关于拓扑排序,我们来看一下下面这张图片:
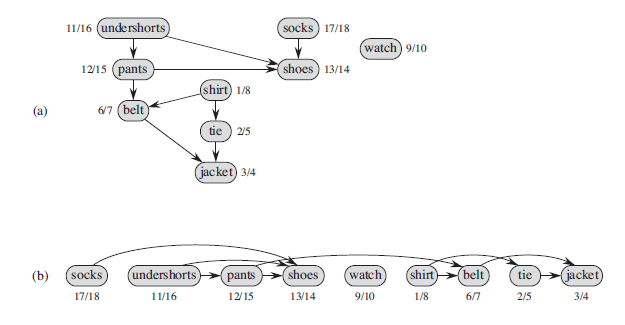
Toplogical Sorting
我们可以用队列来实现这个算法,具体改进的过程如下:
- 记录每个点的入度;
- 将入度为 0 的顶点加入队列;
- 依次对入度为 0 的点进行删边操作,同时将新得到的入度为零的点加入队列;
- 重复上述操作,直至队列为空。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
| #include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int MAX = 10240;
int N, M, pDegree[MAX];
queue<int> Q;
vector<int> pMap[MAX], pVec;
void TopSort();
int main()
{
cin >> N >> M;
memset(pDegree, 0, sizeof(pDegree));
for(int i = 1; i <= M; i++)
{
int s, e;
cin >> s >> e;
pMap[s].push_back(e); // 有向图
pDegree[e]++; // 计算入度
}
TopSort();
return 0;
}
void TopSort()
{
for(int i = 1; i <= N; i++)
{
if(pDegree[i] == 0) // 入度为0的点入队
{ Q.push(i); }
}
while(!Q.empty())
{
int x = Q.front(); Q.pop();
pVec.push_back(x); // 出队顺序即为拓扑序列
for(int i = 0; i < pMap[x].size(); i++)
{
pDegree[pMap[x][i]]--; // 删边
if(pDegree[pMap[x][i]] == 0) // 新的入度为0的点
{ Q.push(pMap[x][i]); }
}
}
for(int i = 1; i <= N; i++)
{
if(pDegree[i] != 0) // 若存在入度不为0的点,则存在环
{
cout << "Exsit Loop" << endl;
return;
}
}
for(int i = 0; i < pVec.size(); i++) // 顺序输出即为拓扑序列
{ cout << pVec[i] << " "; }
cout << endl;
}
{% endhighlight %}
对于这一问题,我们也可以用DFS来解决它,代码如下:
{% highlight cpp linenos %}
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int MAX = 10240;
int N, M, pVisited[MAX]; // 0-未访问 1-正在访问 2-已访问
vector<int> pMap[MAX], pVec;
void TopSort();
bool DFS(int v);
int main()
{
cin >> N >> M;
for(int i = 1; i <= M; i++)
{
int s, e;
cin >> s >> e;
pMap[s].push_back(e); // 有向图
}
TopSort();
return 0;
}
void TopSort()
{
memset(pVisited, 0, sizeof(pVisited));
for(int i = 1; i <= N; i++) // 所有顶点都访问一遍
{
if(!pVisited[i])
{
if(!DFS(i))
{
cout << "Exsit Loop" << endl;
}
}
}
for(int i = pVec.size() - 1; i >= 0; i--) // 倒序输出拓扑序列
{ cout << pVec[i] << " "; }
cout << endl;
}
bool DFS(int v) // false-有环 true-无环
{
pVisited[v] = 1; // 正在访问
for(int i = 0; i < pMap[v].size(); i++) // 搜索它的前驱
{
if(pVisited[pMap[v][i]] == 1) { return false; } // 该点进入两次则有环
else if(pVisited[pMap[v][i]] == 0)
{
if(!DFS(pMap[v][i])) { return false; }
}
}
pVisited[v] = 2; // 访问完毕
pVec.push_back(v); // 加入拓扑序列
return true;
}
|
相较这两种算法,我更倾向于用队列来实现,毕竟这种方法符合求解拓扑排序的一般思路。至于这两种算法的复杂度,在这里就不再分析了。