最近开始准备 NOIP 复赛,发现很多算法已经不会了。只能一个个的捡起来,慢慢复习,顺便做点笔记。
最小生成树(Minimum Spanning Trees),简称 MST。是图论中一个非常重要的概念。解决这个问题有两种算法,今天暂且先来讨论一下 Prim Algorithm。不做特别说明,讨论的都是无向图。
首先介绍一下最小生成树的概念,我们知道,图可以这样定义 $ G=\left(V,E\right) $ ,其中 $ G $ 表示图, $ V $ 表示顶点集合, $ E $ 表示边集合。最小生成树是这样一棵树,它满足 $$ w\left ( T \right )=\min {\left \{ \sum_{\left ( u,v \right )\in T}w\left ( u,v \right ) \right \}} $$ 通俗地讲,就是使得图 $ G $ 连通时,所选取的边的长度的和最小。
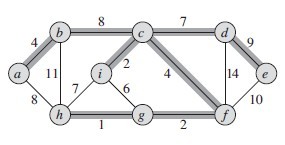
最小生成树
如上图,加粗的路径就是在最小生成树上的路径。
现在,我们开始讨论Prim Algorithm。这个算法可以分为下面几个步骤:
- 将顶点集 $ V $ 分成两个集合 $ A $ 和 $ B $ ,其中集合 $ A $ 表示目前已经在MST中的顶点,而集合 $ B $ 则表示目前不在 MST 中的顶点。
- 寻找与集合 $ A $ 连通的最短的边 $ \left(u,v\right) $ ,将这条边加入最小生成树中。(此时,与 $ \left(u,v\right) $ 相连的顶点,不妨设为 $ B_{i} $ ,也应加入集合 $ A $ 中)
- 重复第二步,直至集合 $ B $ 为空集。
算法的大体思想就是这样了。为了方便理解,我们先来看一下下面一张图片:
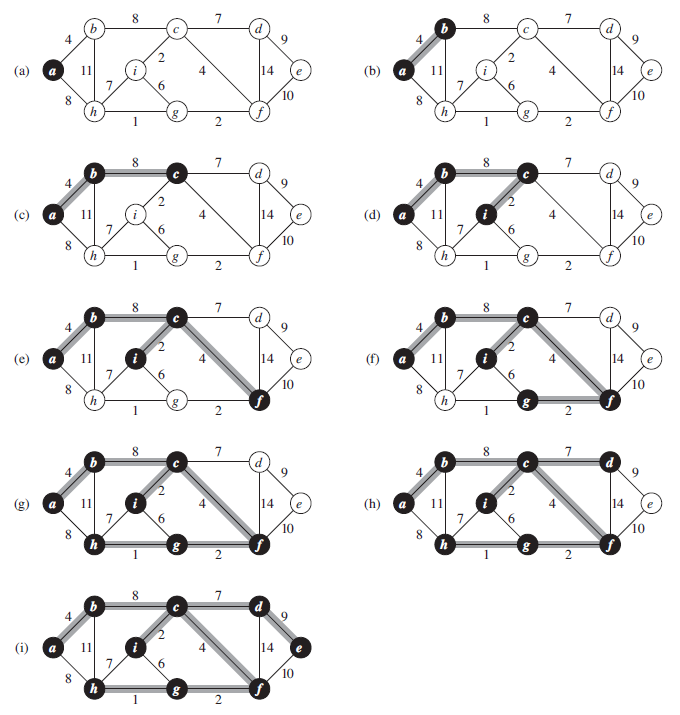
Prim 算法
对照上面的图片,想必对于 Prim Algorithm 也有了一定的理解。
下面我们来设计算法,显然,我们需要遍历集合 $ A $ 中所有顶点及与之相连的边,取连接到集合 $ B $ 的权值最小的边,加入最小生成树。这样一来,复杂度将达到 $ O\left(n^{3}\right) $ 。
我们可以对这个想法进行优化。我们维护一个 $ pCost\left [ i \right ] $ 数组,用来表示从集合 $ A $ 到与之相邻的节点的最小费用。这样,我们只要每次取这个数组中的最小值,把它在集合 $ B $ 中所对应的结点 $ V_{i} $ 加入到集合 $ A $ 中。每次加入结束以后,都要更新 $ pCost\left [ i \right ] $ 数组。即枚举所有与结点 $ V_{i} $ 相连的边,判断是否比 $ pCost\left [ i \right ] $ 数组中的最小费用小,如果比它小,则更新。这样可以将算法优化到 $ O\left(n^{2}\right) $ 。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include <iostream>
#include <memory.h>
#include <vector>
using namespace std;
const int MAX = 1024;
const int INF = 2147483647; // 设置最大权值
int N, M;
vector<pair<int, int> > pMap[MAX]; // 邻接表
void Prim();
int main()
{
cin >> N >> M;
for(int i = 1; i <= M; i++)
{
int u, v, w;
cin >> u >> v >> w;
pMap[u].push_back(make_pair(v, w));
pMap[v].push_back(make_pair(u, w));
}
Prim();
return 0;
}
void Prim()
{
int nCost = 0;
vector<int> pMST; // 储存MST的结点
int pCost[MAX]; // 储存与集合A相邻的顶点的最小权值,0表示该结点已经在MST中
pMST.push_back(1); // 将结点1加入MST
pCost[1] = 0;
for(int i = 2; i <= N; i++) // 初始化,切记要将除1以外的都置为INF
{ pCost[i] = INF; }
for(int i = 0; i < pMap[1].size(); i++) // 处理与结点1相连的顶点
{ pCost[pMap[1][i].first] = pMap[1][i].second; }
for(int i = 1; i <= N - 1; i++) // 剩余N-1个顶点,循环N-1次
{
int nVertex = 0, nWeight = INF; // 用于寻找最短的边
for(int j = 1; j <= N; j++)
{
if(nWeight > pCost[j] && pCost[j] != 0)
{
nVertex = j;
nWeight = pCost[j];
}
}
pCost[nVertex] = 0;
pMST.push_back(nVertex); // 将节点nVertex加入MST
nCost += nWeight; // 计算MST的费用
for(int j = 0; j < pMap[nVertex].size(); j++) // 更新pCost数组
{
if(pCost[pMap[nVertex][j].first] != 0 &&
pCost[pMap[nVertex][j].first] > pMap[nVertex][j].second)
{
pCost[pMap[nVertex][j].first] = pMap[nVertex][j].second;
}
}
}
cout << "MST Cost is " << nCost << endl;
cout << "The vertexs in MST are ";
for(int i = 0; i < pMST.size(); i++)
{ cout << pMST[i] << " "; }
cout << endl;
}
|