算法专题：最小生成树

今天来介绍一下最小生成树的另外一种算法：Kruskal Algorithm。这个算法是基于贪心实现的，算法的大体过程如下：

取权值最小的边，如果加入这条边以后，不会出现环，那么就加入这条边。
重复上述操作，直至加入了 $ N-1 $ 条边。

我们还是先来看一张图片来理解一下这个算法：

下面我们来考虑这个算法，最棘手的问题是判断是否构成环，这里我们采用并查集来处理这个问题，它的复杂度是 $ O\left(V*\alpha\left(V\right)\right) $ 。对于每次寻找权值最小的边，复杂度是 $ O\left(E\right) $ 。这样一来，复杂度将高达 $ O\left(V*\alpha\left(V\right)+VE\right) $ ，即 $ O\left(VE\right) $ 。

我们考虑优化，每次寻找权值最小的边，可以考虑先将权值从小到大排序。这样复杂度就下降到 $ O\left(V*\alpha\left(V\right)+E\log{E}\right) $ ，即 $ O\left(E\log{E}\right) $ 。

代码如下：

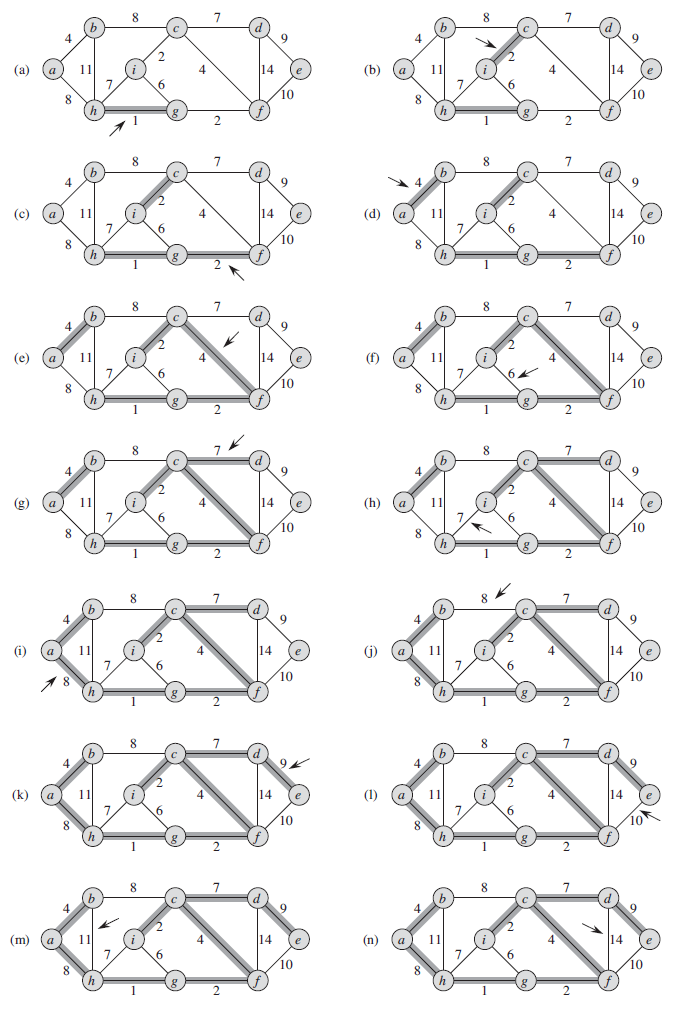
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int MAX = 1024;

struct Edge
{
    Edge(int _u, int _v, int _w)
    {
        u = _u; v = _v; w = _w;
    }

    int u, v, w;
};

struct Set
{
    int nParent, nCount;
};

int cmp(Edge x, Edge y)
{
    return x.w < y.w;
}

int N, M;
vector<Edge> pEdge;
Set pSet[MAX];

void Kruskal();
void Init();
int Find(int x);
void Union(int x, int y);

int main()
{
    cin >> N >> M;
    for(int i = 1; i <= M; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        pEdge.push_back(Edge(u, v, w));
    }
    Kruskal();
    return 0;
}

void Kruskal()
{
    int nCost = 0, nPos = 0;
    vector<Edge> pMST;
    sort(pEdge.begin(), pEdge.end(), cmp);
    Init();
    while(pMST.size() != N - 1)    // 直到MST中有N-1条边
    {
        Edge minEdge = pEdge[nPos++];
        if(Find(minEdge.u) != Find(minEdge.v))    // 如果加入后不构成环
        {
            nCost += minEdge.w;
            pMST.push_back(minEdge);
            Union(minEdge.u, minEdge.v);
        }
    }
    cout << "The MST Cost is " << nCost << endl;
} 

void Init()
{
    for(int i = 1; i <= N; i++)
    {
        pSet[i].nParent = i;
        pSet[i].nCount = 1;
    }
}

int Find(int x)
{
    if(pSet[x].nParent != x)
    {
        return pSet[x].nParent = Find(pSet[x].nParent);        // 路径压缩
    }
    else
    {
        return x;
    }
}

void Union(int x, int y)
{
    int fx = Find(pSet[x].nParent);
    int fy = Find(pSet[y].nParent);
    if(fx != fy)    // 启发式合并，减小树的高度
    {
        if(pSet[fx].nCount > pSet[fy].nCount)
        {
            pSet[fy].nParent = fx;
            pSet[fx].nCount += pSet[y].nCount;
        }
        else
        {
            pSet[fx].nParent = fy;
            pSet[fy].nCount += pSet[x].nCount;
        }
    }
}

至此，最小生成树的算法基本复习完毕。

分析两种算法，Prim Algorithm的复杂度是 $ O\left(V^{2}\right) $ ，适用于稠密图；而Kruskal Algorithm的复杂度是 $ O\left(E\log{E}\right) $ ，适用于疏密图。各有所长，需要根据不同的情况选择不同的算法。

算法专题：最小生成树 – Kruskal Algoritm

介绍了 Kruskal Algorithm 求解最小生成树问题的步骤与代码实现，适用于 NOIP 等编程竞赛备赛复习。