这次我们来讨论一下关于多源最短路径 APSP(All-Pairs Shortest Paths)。即求出给定的图 $ G=\left ( V,E \right ) $ 中任意两对顶点 $ V_{i},V_{j} $ 之间的最短路径。我们根据下面这幅图来理解一下这个概念:
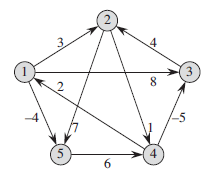
多源最短路径
对于这一问题,比较有效的算法是 Floyd-Warshall Algorithm,简称 Floyd。它是基于动态规划的一种最短路径的算法。
我们用 $ f^{k}\left ( i,j \right ) $ 来表示从顶点 $ i $ 到顶点 $ j $ 不经过索引比 $ k $ 大的点的最短路径。这样一来,我们就可以根据 $ f^{k-1}\left ( i,j \right ) $ 推出 $ f^{k}\left ( i,j \right ) $ 。
假设我们目前已知 $ f^{k-1}\left ( i,j \right ) $ ,要推出 $ f^{k}\left ( i,j \right ) $ ,无外乎两种情况:
- 经过顶点 $ k $ ;
- 不经过顶点 $ k $ 。
对于第一种情况,显然有 $ f^{k}\left ( i,j \right )=f^{k-1}\left ( i,k \right )+f^{k-1}\left ( k,j \right ) $ 。对于第二种情况,我们也很容易得到 $ f^{k}\left ( i,j \right )=f^{k-1}\left ( i,j \right ) $ 。这样一来,状态转移方程也就确定了:
$$ f^{k}\left ( i,j \right )=\min{\left \{ f^{k-1}\left ( i,k \right )+f^{k-1}\left ( k,j \right ),f^{k-1}\left ( i,j \right ) \right \}} $$
这样一来,也就解决了为什么 Floyd-Warshall Algorithm 的最外层循环必须是 $ k $ 这一问题。很显然,Floyd-Warshall Algorithm 的时间复杂度为 $ O\left(V^{3}\right) $ 。
当然,这个算法还可以用来求最小环,具体求法请参考代码,应该能看懂,就不再多说。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include <iostream>
using namespace std;
const int MAX = 10240;
const int INF = 65536;
int N, M;
int f[MAX][MAX], pMap[MAX][MAX];
void Floyd();
int main()
{
cin >> N >> M;
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= N; j++)
{
pMap[i][j] = f[i][j] = (i == j) ? 0 : INF; // 初始化
}
}
for(int i = 1; i <= M; i++)
{
int s, e, v;
cin >> s >> e >> v;
pMap[s][e] = v; pMap[e][s] = v; // 无向图
f[s][e] = v; f[e][s] = v;
}
Floyd();
return 0;
}
void Floyd()
{
int nLen = 65536;
for(int k = 1; k <= N; k++) // 最外层必须是k
{
for(int i = 1; i <= k; i++) // 求解最小环
{
for(int j = 1; j <= k; j++)
{
nLen = min(nLen, pMap[i][j] + f[i][k] + f[k][j]);
}
}
for(int i = 1; i <= N; i++) // 求解APSP
{
for(int j = 1; j <= N; j++)
{
if(f[i][k] + f[k][j] < f[i][j]) // 是否需要松弛
{
f[i][j] = f[i][k] + f[k][j];
}
}
}
}
cout << "Shortest Loop is " << nLen << endl;
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= N; j++)
{
if(f[i][j] == INF)
{ cout << "-1 "; }
else
{ cout << f[i][j] << " "; }
}
cout << endl;
}
}
|

