上一篇文章介绍了一下 Dijkstra Algorithm,但是它仅局限于处理非负权值的图。若图中出现负边,Dijkstra Algorithm 就会出现错误。这时候就需要使用其他的算法来求解单源最短路径。
Ballman-Ford 是一个非常实用的算法,它是由美国数学家 Richard Ballman 和 Lester Ford 发明的。Ballman-Ford 算法的基本流程如下:
初始化 $ pDist\left [ \right ] $ 数组。
检查每一条边,如果源点到该条边的起点有通路,则更新原点到该条边的终点的最短路径。循环 $ V $ 次即可得到结果。
如若要检测是否存在负环,则再检查每一条边,若可以松弛,则有负环。
我们来看一张图片具体体会一下 Bellman-Ford Algorithm:
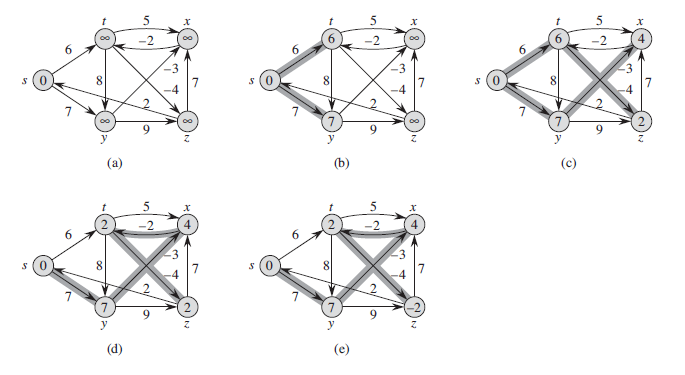
Bellman-Ford 算法
这个算法相对而言比较容易实现,复杂度为 $ O\left ( VE \right ) $ 。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| #include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int MAX = 10240;
const int INF = 2147483647;
struct Edge
{
Edge(int _s, int _e, int _v)
{
s = _s; e = _e; v = _v;
}
int s, e, v;
};
int N, M;
int pDist[MAX];
vector<Edge> pEdge; // 边集数组
void Ford(int s);
int main()
{
cin >> N >> M;
for(int i = 1; i <= M; i++)
{
int s, e, v;
cin >> s >> e >> v;
pEdge.push_back(Edge(s, e, v)); // 无向图
pEdge.push_back(Edge(e, s, v));
}
Ford(1);
return 0;
}
void Ford(int s)
{
bool bNativeLoop = false; // 记录是否存在负环
for(int i = 1; i <= N; i++) // 初始化
{ pDist[i] = INF; }
pDist[s] = 0;
for(int i = 1; i <= N; i++) // 循环N次
{
for(int j = 0; j < pEdge.size(); j++) // 每次检查每一条边
{
int s = pEdge[j].s, e = pEdge[j].e, v = pEdge[j].v;
if(pDist[s] != INF) // 如果源点可以到达顶点s则进行松弛
{
pDist[e] = min(pDist[e], pDist[s] + v);
}
}
}
for(int i = 0; i < pEdge.size(); i++) // 检查负环
{
int s = pEdge[i].s, e = pEdge[i].e, v = pEdge[i].v;
if(pDist[e] > pDist[s] + v) // 若松弛完毕后还能松弛,则存在负环
{
bNativeLoop = true;
break;
}
}
if(bNativeLoop == true) { cout << "Exist Native Loop" << endl; }
else
{
for(int i = 1; i <= N; i++)
{
cout << pDist[i] << " ";
}
cout << endl;
}
}
|