前几天在数学组听课的时候,做平面几何的题目,遇到了塞瓦定理。当时赵诚宇给我讲了一遍,现在再把它整理一下。
塞瓦定理:在 $\triangle ABC$ 中,若线段 $AD$、$BE$、$CF$ 通过同一点 $O$,则 $\frac {BD} {DC} \cdot \frac {CE} {EA} \cdot \frac {AF} {FB} =1$。
塞瓦定理逆定理:在 $\triangle ABC$ 中,若点 $D$、$E$、$F$ 分别在边 $AD$、$BE$、$CF$ 上,且满足 $\frac {BD} {DC} \cdot \frac {CE} {EA} \cdot \frac {AF} {FB} =1$,则线段 $AD$、$BE$、$CF$ 共点或彼此平行。(我们在此只研究共点的情形)
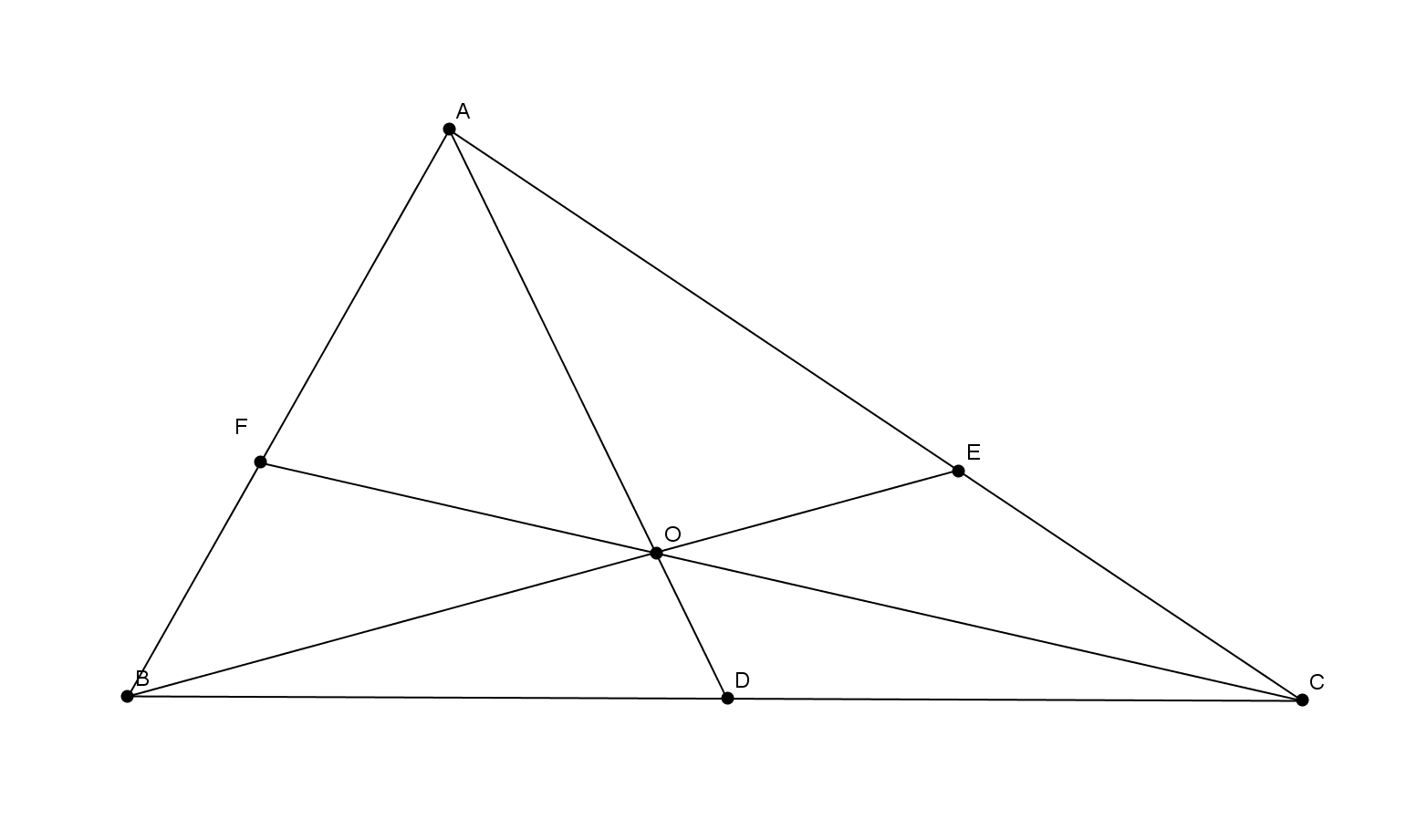
Ceva 定理示意图
证明如下:
首先 $$\frac {BD} {DC}=\frac {S_{\triangle ABD}}{S_{\triangle ADC}}=\frac {S_{\triangle OBD}}{S_{\triangle ODC}} \Rightarrow \frac {BD} {DC}=\frac {S_{\triangle ABD}-S_{\triangle OBD}}{S_{\triangle ADC}-S_{\triangle ODC}}=\frac {S_{\triangle ABO}}{S_{\triangle CAO}}$$ 同理 $$\frac {CE} {EA}=\frac {S_{\triangle BCO}}{S_{\triangle ABO}},\frac {AF} {FB}=\frac {S_{\triangle CAO}}{S_{\triangle BCO}}$$ 因此 $$\frac {BD} {DC} \cdot \frac {CE} {EA} \cdot \frac {AF} {FB} = \frac{S_{\triangle ABO}}{S_{\triangle CAO}} \cdot \frac{S_{\triangle BCO}}{S_{\triangle ABO}} \cdot \frac{S_{\triangle CAO}}{S_{\triangle BCO}}=1$$ 证毕。
例:在筝形 $ABCD$ 中,$AB=AD$,$BC=CD$,经 $AC$、$BD$ 的交点 $O$ 任做两条直线,分别交 $AD$ 于 $E$,交 $CD$ 于 $H$。$GF$、$EH$ 分别交 $BD$ 于 $I$,$J$。求证:$IO=OJ$。
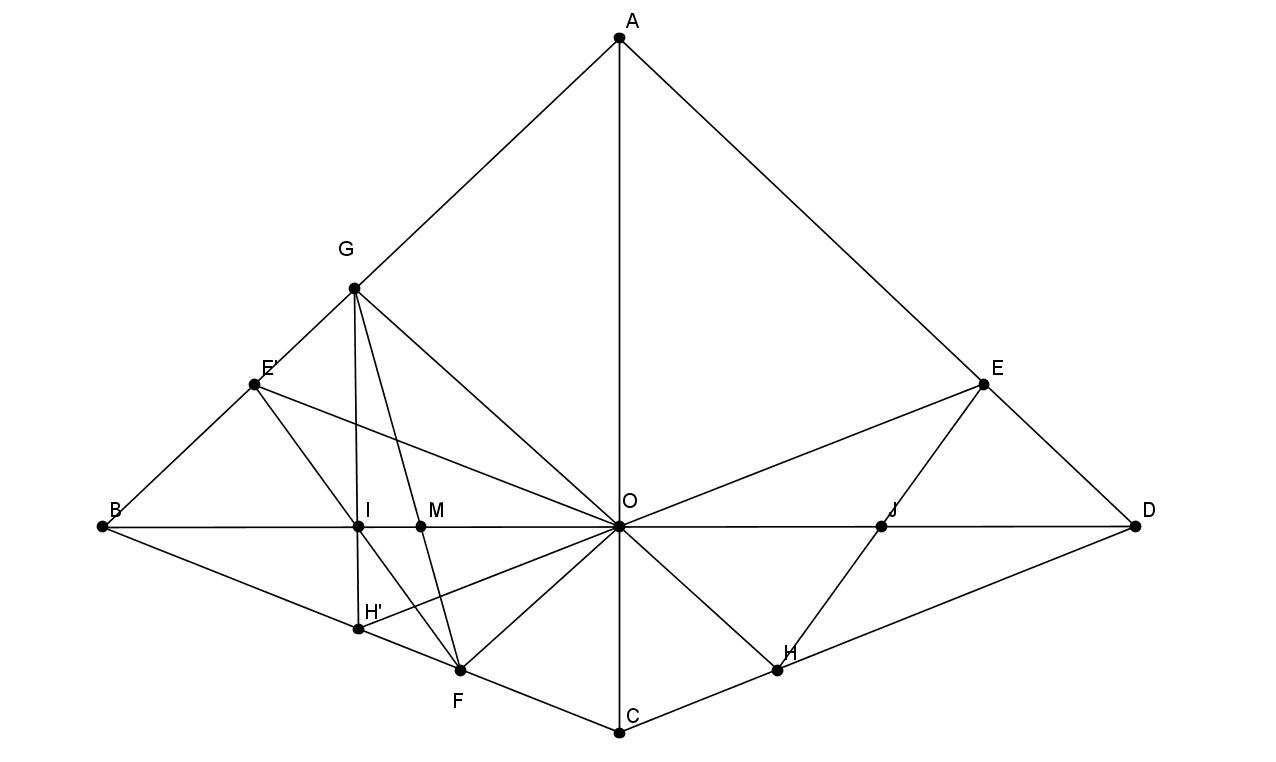
Ceva 定理例题图
证明如下:
作 $\triangle ABC$ 的关于 $AC$ 的对称图形,记 $E^{’}H^{’} \cap BB=M$ 设 $\angle GOB=\angle BOH^{’}=\alpha,\angle E^{’}OG=\angle FOH^{’}=\beta$ 则有:$$\frac{E^{’}G}{GB} \cdot \frac{BH^{’}}{H^{’}F} \cdot \frac{FM}{ME^{’}}=\frac{OE^{’}\sin \beta}{OB \sin \alpha} \cdot \frac{OB \sin \alpha}{OF \sin \beta} \cdot \frac{OF \sin \left ( \alpha + \beta \right )}{OE^{’} \sin \left ( \alpha + \beta \right )}=1$$ 由塞瓦定理得:$MB$、$E^{’}H^{’}$、$GF$ 共点,因此 $IO=OJ$。证毕。
