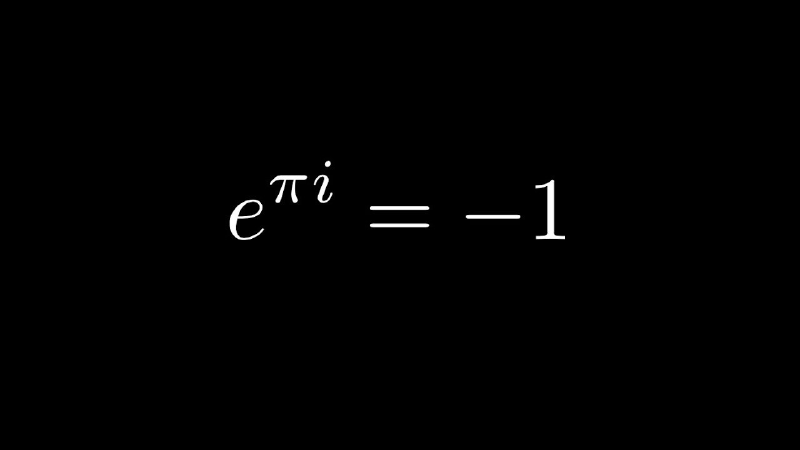新版高中教材对复数内容进行了极大的删减,使得我们对于复数的认知还停留在最原始的阶段。殊不知,复数的应用非常广泛。现参考《高中数学·甲种本》以及搜集的一些资料,包括做过的例题,整理一下关于复数的内容。
一、复数的概念
1.1 数的概念的发展
数的概念是从实践中产生和发展起来的。早在原始社会末期,由于记数的需要,人们就建立起自然熟的概念。自然数的全体构成自然数集$\mathbf{N}$。
随着生产和科学的发展,熟的概念也得到了发展。
为了表示各种具有相反意义的量以及满足记数法的要求,人们引进了零和负数,把自然数看作正整数,把正整数、零、负整数合并在一起,构成整数集$\mathbf{Z}$。
为了解决测量、分配中遇到的将某些量进行等分的问题,人们又引进了有理数,规定他们就是一切形如$\frac{m}{n}$的数,其中$m\in \mathbf{Z},n\in \mathbf{N}$。这样,就把整数集$\mathbf{Z}$扩大为有理数集$\mathbf{Q}$。显然,$\mathbf{Z}\subset \mathbf{Q}$。如果把整数看作分母为$1$的分数,那么有理数实际上就是分数集。
每一个有理数都可以表示成整数、有限小数或循环节不为$0$的循环小数;反过来,整数、有限小数或循环节不为$0$的循环小数也都是有理数。如果把整数、有限小数都看作循环节为$0$的循环小数,那么有理数集实际上就是循环小数的集合。
为了解决有些量与量之间的比值(例如用正方形的边长去度量它的对角线所得结果)不能用有理数表示的矛盾,人们又引入了无理数。所谓无理数,就是无限不循环小数。有理数集与无理数集合并在一起,构成实数集$\mathbf{R}$。因为有理数都可以看作循环小数(包括整数、有限小数),无理数都是无限不循环小数,所以实数集就是小数集。
从解方程来看,方程$x+5=3$在自然数集$\mathbf{N}$中无解,在整数集$\mathbf{Z}$中就有一个解$x=-2$;方程$3x=5$字整数集$\mathbf{Z}$中无解,在有理数集$\mathbf{Q}$中就有一个解$x=\frac{5}{3}$;方程$x^{2}=2$在有理数集$\mathbf{Q}$中无解,在实数集$\mathbf{R}$中就有两个解$x=\pm \sqrt{2}$。但是,熟的范围扩充到实数集$\mathbf{R}$以后,象$x^{2}=-1$这样的方程还是无解,因为没有一个实数的平方等于$-1$。在十六世纪,由于解方程的需要,人们开始引进一个新数$i$,叫做虚数单位,并规定:
它的平方等于$-1$,即
$$ i^{2}=-1 $$
实数与它进行四则运算时,所有的加、乘运算律仍然成立。
在这种规定下,$i$可以与实数$b$相乘,再同实数$a$相加,由于满足乘法交换律及加法交换律,从而可以把结果写成$a+bi$。人们把它们叫做复数。全体复数所成的集合,一般用字母$\mathbf{C}$来表示。1
在这种规定下,$i$就是$-1$的一个平方根。因此,方程$x^{2}=-1$在复数集$\mathbf{C}$中就至少有一个解$x=i$。
十八世纪以后,复数在数学、力学和电学中得到了应用。从此对它的研究日益展开。现在复数已成为科学技术中普遍使用的一种数学工具。
1.2 复数的有关概念
复数$a+bi$($a,b\in\mathbf{R}$。以后说复数$a+bi$时,都有$a,b\in\mathbf{R}$),当$b=0$时,就是实数;当$b\neq 0$时,叫做虚数,当$a=0,b\neq 0$时,叫做纯虚数;$a$与$b$分别叫做复数$a+bi$的实部与虚部。例如,$3+4i,-\frac{1}{2}-\sqrt{2}i,-0.5i$都是虚数,它们的实部分别是$3,-\frac{1}{2},0$,虚部分别是$4,-\sqrt{2},-0.5$。
显然,实数集$\mathbf{R}$是复数集$\mathbf{C}$的真子集,即$\mathbf{R}\subset \mathbf{C}$。
如果两个复数$a+bi$与$c+di$的实部与虚部分别相等,我们就说这两个复数相等,记作$a+bi=c+di$,这就是说,如果$a,b,c,d\in\mathbf{R}$,那么 $$ a+bi=c+di \Leftrightarrow a=c,b=d $$ $$ a+bi=0\Leftrightarrow a=b=0 $$
例:已知$\left ( 2x-1 \right )+i=y-\left ( 3-y \right )i$,其中$x,y\in\mathbf{R}$。求$x$与$y$。
解:根据复数相等的定义,得方程组$\begin{cases} 2x-1=y,\\ 1=-\left ( 3-y \right ) \end{cases}$解得$x=\frac{5}{2},y=4$。
从复数相等的定义,我们知道,任何一个复数$z=a+bi$,都可以由一个有顺序的实数对$\left ( a,b \right )$唯一确定。这就使我们能借用平面直角坐标系来表示复数$z=a+bi$。如图1,点$Z$的横坐标是$a$,纵坐标是$b$,复数$z=a+bi$可用点$Z\left ( a,b \right )$来表示。这个建立了直角坐标系表示复数的平面叫做复平面,$x$轴叫做实轴,$y$轴除去原点的部分叫做虚轴(因为原点表示实数$0$,原点不在虚轴上)。表示实数的点都在实轴上,表示纯虚数的点都在轴上。
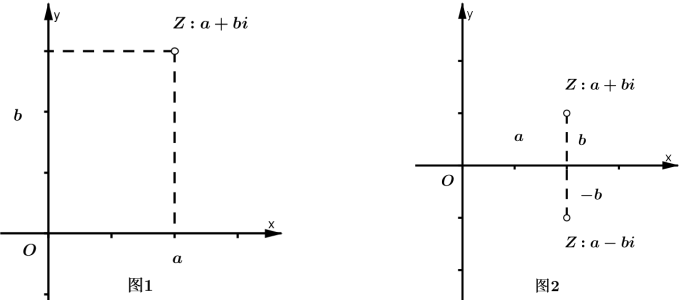
复数的复平面表示法
很明显,按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应;反过来,复平面内的每一个点,有唯一的一个复数和它对应。由此可知,复数集$\mathbf{C}$和复平面内所有的点所成的集合是一一对应的。这是复数的一个几何意义。
当两个复数实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数(当虚部不等于$0$时也叫做互为共轭虚数)。复数$z$的共轭复数可以用$\overline{z}$来表示,也就是说,复数$z=a+bi$的共轭复数是$\overline{z}=a-bi$。显然,复平面内表示两个互为共轭复数的点$Z$与$\overline{Z}$关于实轴对称(图2),而实数$a$(即虚部为$0$的复数)的共轭复数仍是$a$本身。
两个实数可以比较大小。但是两个复数,如果不全是实数,就不能比较它们的大小。对于这个命题的证明,将稍后给出。
1.3 复数的向量表示
在物理学中,我们经常遇到力、速度、加速度、电场强度等,这些量,除了要考虑它们的绝对值大小以外,还要考虑它们的方向。我们把这种既有绝对值大小又有方向的量叫做向量。向量可以用有向线段来表示,线段的长度就是这个向量的绝对值(叫做这个向量的模),线段的方向(用箭头表示)就是这个向量的方向。模相等且方向相同的向量,不管它们的起点在哪里,都认为是相等的向量。在这一规定下,向量可以根据需要进行平移。模为零的向量(它的方向是任意的)叫做零向量。规定所有零向量相等。

复数的向量表示法
复数可以用向量来表示。如图 3,设复平面内的点$Z$表示复数$z=a+bi$,连结$OZ$,如果我们把有向线段$OZ$(方向是从点$O$指向点$Z$)看成向量,记作$\overrightarrow{OZ}$,就把复数同向量联系起来了。很明显,向量$\overrightarrow{OZ}$是由点$Z$唯一确定的;反过来,点$Z$也可由向量$\overrightarrow{OZ}$唯一确定。因此,复数集$C$与复平面内所有以原点$O$为起点的向量所成的集合也是一一对应的。为方便起见,我们常把复数$z=a+bi$说成点$Z$或者说成向量$\overrightarrow{OZ}$。此外,我们还规定,相等的向量表示同一个复数。
图3中的向量$\overrightarrow{OZ}$的模(即有向线段$OZ$的长度)$r$叫做复数$z=a+bi$的模(或绝对值)记作 $\left | z \right |$或$\left | a+bi \right |$ 。如果$b=0$,那么$z=a+bi$是一个实数$a$它的模就等于 $\left | a \right |$ (即$a$在实数意义上的绝对值)。容易看出,
$\left | z \right |=\left | a+bi \right |=r=\sqrt{a^{2}+b^{2}}.$
例1:求复数$z_{1}=3+4i$及$z_{2}=-\frac{1}{2}-\sqrt{2}i$的模,并且比较它们的模的大小。
解: $\left| z_{1} \right|=\sqrt{3^{2}+4^{2}}=5,\left | z_{2} \right |=\sqrt{\left ( -\frac{1}{2} \right )^{2}+\left ( \sqrt{2} \right )^{2}}=\frac{3}{2}.$又$5 > \frac{3}{2}$ ,故$\left | z_{1} \right | > \left | z_{2} \right |$。
例2:设$z\in\mathbf{C}$,满足下列条件的点$Z$的集合是什么图形? (1)$\left | z \right |=4$;(2)$2 < \left | z \right | < 4$。
解:
(1)复数$z$的模等于$4$,就是说,向量$\rightarrow{OZ}$的模(即点$Z$与原点$O$的距离)等于$4$,所以满足条件 $\left | z \right |=4$ 的点$Z$的集合是以原点$O$为圆心,以$4$为半径的圆。
(2)不等式$2 < \left | z \right | < 4$可化为不等式组$\begin{cases}\left | z \right | < 4\\ \left | z \right | > 2\end{cases}$。不等式$\left | z \right | < 4$的解集是圆$\left | z \right | = 4$内部所有的点组成的集合,不等式$\left | z \right | > 2$的解集是圆$\left | z \right | = 2$外部所有的点组成的集合,这两个集合的交集,就是上述不等式组的解集,也就是满足条件$2 < \left | z \right | < 4$的点$Z$的集合。容易看出,所求的集合是以原点$O$为圆心,以$2$及$4$为半径的圆所夹的圆环,但不包括圆环的边界(图 4)。

圆
二、复数的运算
2.1 复数的加法与减法
复数的加法规定按照以下的法则进行:设$z_{1}=a+bi,z_{2}=c+di$是任意两个复数,那么它们的和:$$ \left ( a+bi \right )+\left ( c+di \right )=\left ( a+c \right )+\left ( b+d \right )i $$ 很明显,两个复数的和仍然是一个复数。
容易验证,复数的加法满足交换律、结合律,即对任意$z_{1},z_{2},z_{3}\in\mathbf{R}$,有 $$ z_{1}+z_{2}=z_{2}+z_{1} $$ $$ \left ( z_{1}+z_{2} \right )+z_{3}=z_{1}+\left ( z_{2}+z_{3} \right ) $$ 现在我们来看复数加法的几何意义。
从物理学知道,要求出作用于同一点$O$、但不在同一直线上的两个力$\overrightarrow{F_{1}}$与$\overrightarrow{F_{2}}$的合力,只要用表示$\overrightarrow{F_{1}}$与$\overrightarrow{F_{2}}$的向量为相邻的两边画一个平行四边形,那么,平行四边形中,以力的作用点$O$为起点的那条对角线所表示的向量就是合力$\overrightarrow{F}$(图5-1)。这个法则通常叫做向量加法的平行四边形法则。
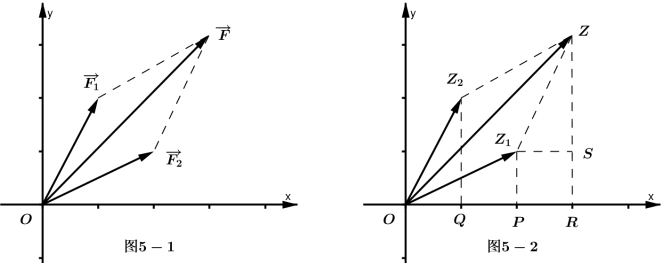
复数加法的几何意义
复数用向量来表示,如果与这些复数对应的向量不在同一直线上,那么这些复数的加法就可以按照向量加法的平行四边形法则来进行。下面我们来证明这一事实。
设$\overrightarrow{OZ_{1}}$及$\overrightarrow{OZ_{2}}$分别与复数$a+bi$及$c+di$对应,且$\overrightarrow{OZ_{1}},\overrightarrow{OZ_{2}}$不在同一直线上(图5-2)。以$\overrightarrow{OZ_{1}}$及$\overrightarrow{OZ_{2}}$为两条邻边画平行四边形$OZ_{1}ZZ_{2}$,画$x$轴的垂线$PZ_{1},QZ_{2}$及$RZ$,并且画$Z_{1}S\perp RZ$,容易证明
$\triangle ZZ_{1}S\cong \triangle Z_{2}OQ,$
并且四边形$Z_{1}PRS$是矩形,因此
$OR=OP+PR=OP+Z_{1}S=OP+OQ=a+c$
$RZ=RS+SZ=PZ_{1}+QZ_{2}=b+d.$
于是点$Z$的坐标是$\left ( a+c,b+d \right )$,这说明设$\overrightarrow{OZ}$就是于复数$\left ( a+c \right )+\left ( b+d \right )i$对应的向量。
由此可知,求两个复数的和,可以先画出这两个复数对应的向量$\overrightarrow{OZ_{1}},\overrightarrow{OZ_{2}}$,如果$\overrightarrow{OZ_{1}},\overrightarrow{OZ_{2}}$不在同一直线上,再以这两个向量为两条邻边画平行四边形,那么与这个平行四边的对角线$OZ$所表示的向量$\overrightarrow{OZ}$对应的复数,就是所求两个复数的和。
如果$\overrightarrow{OZ_{1}},\overrightarrow{OZ_{2}}$在同一直线上,我们可以画出一个“压扁”了的平行四边形,并据此画出它的对角线来表示$\overrightarrow{OZ_{1}},\overrightarrow{OZ_{2}}$的和。
总之,复数的加法可以按照向量的加法法则来进行,这是复数加法的几何意义。
下面再来看复数的减法。
复数的减法规定是加法的逆运算,即把满足 $$ \left ( c+di \right )+\left ( x+yi \right )=a+bi $$ 的复数$x+yi$,叫做复数$a+bi$减去复数$c+di$的差。记作$\left ( a+bi \right )-\left ( c+di \right )$,根据复数相等的定义,有 $$ c+x=a,d+y=b $$ 由此 $$ x=a-c,y=b-d, $$ 所以 $$ x+yi=\left ( a-c \right )+\left ( b-d \right )i, $$ 即 $$ \left ( a+bi \right )-\left ( c+di \right )=\left ( a-c \right )+\left ( b-d \right )i $$ 这就是复数的减法法则。由此可见,两个复数的差是一个唯一确定的复数。
现设$\overrightarrow{OZ}$与复数$a+bi$对应,$\overrightarrow{OZ_{1}}$与复数$c+di$对应(图6)。以$\overrightarrow{OZ}$为一条对角线,$\overrightarrow{OZ_{1}}$为一条边画平行四边形,那么这个平行四边形的另一边,$\overrightarrow{OZ_{2}}$所表示的向量,$\overrightarrow{OZ_{2}}$就与复数$\left ( a-c \right )+\left ( b-d \right )i$对应。因为$Z_{1}Z\stackrel{;//;}{=}OZ_{2}$,所以向量$\overrightarrow{Z_{1}Z}$也与这个差对应。
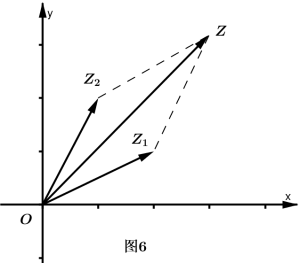
复数减法的几何意义
这就是说,两个复数的差$z-z_{1}$(即$\overrightarrow{OZ}-\overrightarrow{OZ_{1}}$)与连结两个向量终点并指向被减数的向量对应。这就是复数减法的几何意义。
由上所述,我们可以看出,复数的加(减)法与多项式的加(减)法是类似的,就是把复数的实部与实部、虚部与虚部分别相加(减),即
$$ \left ( a+bi \right )\pm \left ( c+di \right )=\left ( a\pm c \right )+\left ( b\pm d \right ) $$
例1:计算$\left ( 5-6i \right )+\left ( -2-i \right )-\left ( 3+4i \right )$。
解:$\left ( 5-6i \right )+\left ( -2-i \right )-\left ( 3+4i \right )=\left ( 5-2-3 \right )+\left ( -6-1-4 \right )i=-11i$。
例2:根据复数的几何意义及向量表示,求复平面内两点间的距离公式。
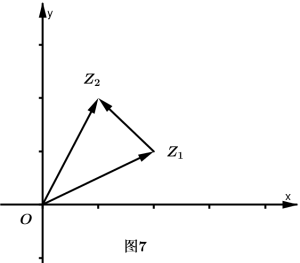
复平面两点距离
解:如图 7,设复平面内的任意两点$Z_{1},Z_{2}$分别表示复数$z_{1}=x_{1}+y_{1}i,z_{2}=x_{2}+y_{2}i$,那么$\overrightarrow{Z_{1}Z_{1}}$就是与复数$z_{2}-z_{1}$对应的向量。如果用$d$表示点$Z_{1},Z_{1}$之间的距离,那么$d$就是向量$\overrightarrow{Z_{1}Z_{2}}$的模,即复数$z_{2}-z_{1}$的模,所以 $$ d=\left | z_{2}-z_{1} \right |=\left | \left ( x_{2}+y_{2}i \right )-\left ( x_{1}+y_{1}i \right ) \right |=\left | \left ( x_{2}-x_{1} \right )+\left ( y_{2}-y_{1} \right )i \right |=\sqrt{\left ( x_{2}-x_{1} \right )^2+\left ( y_{2}-y_{1} \right )^2} $$ 这与我们之前导出的两点间的距离公式一致。
例3:根据复数的几何意义及向量表示,求复平面内的圆的方程。
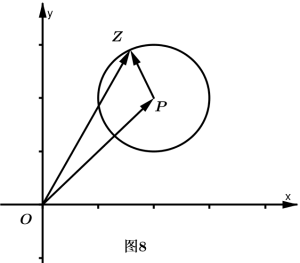
复平面圆
解:如图8,设圆心为$P$,点$P$与复数$p=a+bi$对应,圆的半径为$r$,圆上任意一点$Z$与复数$z=a+bi$对应,那么 $$ \left | z-p \right |=r $$ 这就是复平面内的圆的方程。特别地,当点$P$在原点时,圆的方程就成了 $$ \left | z \right |=r $$
请读者利用复数的减法法则,把圆的方程 $$ \left | z-p \right |=r $$ 化成用实数表示的一般形式 $$ \left ( x-a \right )^{2}+\left ( y-b \right )^{2}=r^{2} $$
2.2 复数的乘法与除法
复数的乘法规定按照以下的法则进行:设$z_{1}=a+bi,z_{2}=c+di$是任意两个复数,那么它们的积 $$ \left ( a+bi \right )\left ( c+di \right )=ac+bci+cdi+bdi^{2}=\left ( ac-bd \right )+\left ( bc+ad \right )i $$
也就是说,复数的乘法与多项式的乘法是类似的,但必须在所得的结果中把$i^{2}$换成$-1$,并且把实部和虚部分别合并。
很显然,两个复数的积仍然是一个复数。
容易验证,复数的乘法满足交换律、结合律以及乘法对加法的分配律,即对任何$z_{1},z_{2},z_{3}\in\mathbf{C}$,有 $$ z_{1}\cdot z_{2}=z_{2}\cdot z_{1} $$ $$ \left ( z_{1}\cdot z_{2} \right )\cdot z_{3}=z_{1}\cdot\left ( z_{2}\cdot z_{3} \right ) $$ $$ z_{1}\cdot \left ( z_{2}+z_{3} \right )=z_{1}\cdot z_{2}+z_{1}\cdot z_{3} $$
根据复数的乘法法则,对于任何复数$z=a+bi$,有 $$ \left ( a+bi \right )\left ( a-bi \right )=a^{2}+b^{2}+\left ( ab-ab \right )i=a^{2}+b^{2} $$
因此,两个共轭复数$z,\overline{z}$的积是一个实数,这个实数等于每一个复数的模的平方,即 $$ z\cdot \overline{z}=\left | z \right |^{2}=\left | \overline{z} \right |^{2} $$
例1:计算$\left ( 1-2i \right )\left ( 3+4i \right )\left ( -2+i \right )$。
解:$\left ( 1-2i \right )\left ( 3+4i \right )\left ( -2+i \right )=\left ( 11-2i \right )\left ( -2+i \right )=-20+15i$。
计算复数的乘方,要用到虚数单位$i$的乘方。因为复数的长发满足交换律与结合律,所以实数集$\mathbf{R}$中正整数指数幂的运算律,在复数集$\mathbf{C}$中仍然成立,即对任何$z,z_{1},z_{2}\in\mathbf{C}$及$m,n\in\mathbf{N}$,有 $$ z^{m}\cdot z^{n}=z^{m+n} $$ $$ \left ( z^{m} \right )^{n}=z^{mn} $$ $$ \left ( z_{1}\cdot z_{2} \right )^{n}=z_{1}^{n}\cdot z_{1}^{n} $$ 另一方面,我们有 $$ i^{1}=i $$ $$ i^{2}=-1 $$ $$ i^{3}=i^{2}\cdot i=-i $$ $$ i^{4}=i^{3}\cdot i=-i\cdot i=-i^{2}=1 $$ 从而,对于任何$n\in\mathbf{N}$,我们都有 $$ i^{4n+1}=i^{4n}\cdot i=\left ( i^4 \right )^{n}\cdot i=1^{n}\cdot i=i $$ 同理可证 $$ i^{4n+2}=-1 $$ $$ i^{4n+3}=-i $$ $$ i^{4n}=1 $$ 这就是说,如果$n\in\mathbf{N}$,那么 $$ i^{4n+1}=i,i^{4n+2}=-1,i^{4n+3}=-i,i^{4n}=1 $$
例2:计算$\left ( \frac{1}{2}-\frac{\sqrt{3}}{2}i \right )^{3}$。
解: $$ \begin{align*} \left ( \frac{1}{2}-\frac{\sqrt{3}}{2}i \right )^{3}&=\left ( \frac{1}{2} \right )^3-3\left ( \frac{1}{2} \right )^{2}\left ( \frac{\sqrt{3}}{2}i \right )+3\left ( \frac{1}{2} \right )\left ( \frac{\sqrt{3}}{2}i \right )^{2}-\left ( \frac{\sqrt{3}}{2} \right )^{3}\\ &=\frac{1}{8}-\frac{3\sqrt{3}}{8}i-\frac{9}{8}+\frac{3\sqrt{3}}{8}i\\ &=-1\end{align*} $$
复数的除法规定是乘法的逆运算,即把满足 $$ \left ( c+di \right )\left ( x+yi \right )=a+bi\left ( c+di\neq 0 \right ) $$ 的复数$x+yi$,叫做复数$a+bi$除以复数$c+di$的商,记作 $$ \left ( a+bi \right )\div \left ( c+di \right ) $$ 或 $$ \frac{a+bi}{c+di} $$
我们知道,两个共轭复数的积是一个实数,因此,两个复数相除,可以先把它们的商写成分式的形式,然后把分子与分母都乘以分母的共轭复数,并且把结果化简,即 $$ \frac{a+bi}{c+di}=\frac{\left ( a+bi \right )\left ( c-di \right )}{\left ( c+di \right )\left ( c-di \right )}=\frac{\left ( ac+bd \right )+\left ( bc-ad \right )i}{c^{2}+d^{2}}=\frac{ac+bd}{c^{2}+d^{2}}+\frac{bc-ad}{c^{2}+d^{2}}i\left ( c+di\neq 0 \right ) $$
因为$c+di\neq 0$,所以$c^{2}+d^{2}\neq 0$。由此可见,商$\frac{a+bi}{c+di}$是一个唯一确定的复数。
例3:计算$\left ( 1+2i \right )\div \left ( 3-4i \right )$。
解:$\left ( 1+2i \right )\div \left ( 3-4i \right )=\frac{1+2i}{3-4i}=\frac{\left ( 1+2i \right )\left ( 3+4i \right )}{\left ( 3-4i \right )\left ( 3+4i \right )}=\frac{-5+10i}{25}=-\frac{1}{5}+\frac{1}{2}i$。
三、复数的三角形式
3.1 复数的三角形式
我们知道,与复数$z=a+bi$对应的向量$\overrightarrow{OZ}$(图9)的模$r$叫做这个复数的模,并且 $$ r=\sqrt{a^{2}+b^{2}} $$
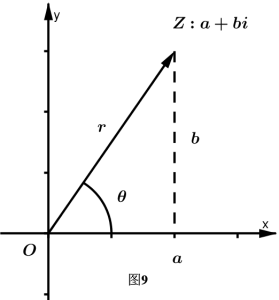
复数的模
以$x$轴的正半轴为始边、向量$\overrightarrow{OZ}$所在的射线(起点是$O$)为终边的角$\theta$,叫做复数$z=a+bi$的辐角。
不等于零的复数$z=a+bi$的辐角有无限多个值,这些值相差$2\pi$的整数倍。例如,复数$i$的辐角是$\frac{\pi}{2}+2k\pi$,其中$k$可以取任何整数。
适合于$0\leq \theta < 2\pi$的辐角$\theta$的值,叫做辐角的主值。记作$\textrm{arg} z$,即$0\leq \textrm{arg} z < 2\pi$。
每一个不等于零的复数有唯一的模与辐角的主值,并且可由它的模与辐角的主值唯一确定。因此,两个非零复数相等当且仅当它们的模与辐角的主值分别相等。
很明显,当$a\in\mathbf{R^{+}}$时,$$ \textrm{arg}\alpha=0 $$ $$ \textrm{arg}\left ( -\alpha \right )=\pi $$ $$ \textrm{arg}\left ( ai \right )=\frac{\pi}{2} $$ $$ \textrm{arg}\left ( -ai \right )=\frac{3\pi}{2} $$ 如果$z=0$,那么与它对应的向量$\overrightarrow{OZ}$缩成一个点(零向量),这样的向量的方向是任意的,所以复数$0$的辐角也是任意的。
从图 9 可以看出: $$ \begin{cases} a=r\cos{\theta}\\ b=r\sin{\theta} \end{cases} $$ 因此 $$ a+bi=r\cos{\theta}+ir\sin{\theta}=r\left ( \cos{\theta}+i\sin{\theta} \right ) $$ 其中 $$ r=\sqrt{a^{2}+b^{2}},\cos{\theta}=\frac{a}{r},\sin{\theta}=\frac{b}{r} $$
当与$z$对应的点$Z$不在实轴或虚轴上时,$z$的辐角$\theta$的终边所在的象限就是点$Z$所在的象限;当点$Z$在实轴或虚轴上时,辐角$\theta$的终边就是从原点$O$出发、经过点$Z$的板条坐标轴。
因此我们可以说,任何一个复数$z=a+bi$都可以表示成$r\left ( \cos{\theta}+i\sin{\theta} \right )$的形式。
$$ r\left ( \cos{\theta}+i\sin{\theta} \right ) $$ 叫做复数$a+bi$的三角形式。为了同三角形式区别开来,$a+bi$叫做复数的代数形式。
例1:把复数$\sqrt{3}+i$表示成三角形式。
解:$r=\sqrt{3+1}=2,\cos{\theta}=\frac{\sqrt{3}}{2}.$因为与$\sqrt{3}+i$对应的点在第一象限,所以$\textrm{arg}\left ( \sqrt{3}+i \right )=\frac{\pi}{6}$,于是$\sqrt{3}+i=2\left ( \cos{\frac{\pi}{6}}+i\sin{\frac{\pi}{6}} \right ).$
例2:把复数$1-i$表示成三角形式。
解:$r=\sqrt{1+1}=\sqrt{2},\cos{\theta}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}.$因为与$1-i$对应的点在第四象限,所以$\textrm{arg}\left ( 1-i \right )=\frac{7\pi}{4}$,于是$1-i=\sqrt{2}\left ( \cos{\frac{7\pi}{4}}+i\sin{\frac{7\pi}{4}} \right ).$
例3:把复数$-1$表示成三角形式。
解:$r=\sqrt{1+0}=1.$因为与$-1$对应的点在$x$轴的负半轴上,所以$\textrm{arg}\left ( -1 \right )=\pi$,于是$-1=\cos{\pi}+i\sin{\pi}.$
当然,把一个复数表示成三角形式时,辐角$\theta$不一定要取主值。例如,$\sqrt{2}\left [ \cos{\left ( -\frac{\pi}{4} \right )}+i\sin{\left ( -\frac{\pi}{4} \right )} \right ]$也是复数$1-i$的三角形式。
3.2 复数的三角形式的运算
3.2.1 乘法与乘方
如果把复数$z_{1},z_{2}$分别写成三角形式 $$ z_{1}=r_{1}\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right ) $$ $$ z_{2}=r_{2}\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right ) $$ 故有 $$ \begin{align*} z_{1}\cdot z_{2} &=r_{1}\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right )\cdot r_{2}\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right )\\ &=r_{1}r_{2}\left [ \left (\cos{\theta_{1}}\cos{\theta_{2}}-\sin{\theta_1}\sin{\theta_{2}} \right ) + i\left ( \sin{\theta_{1}}\cos{\theta_{2}}+\cos{\theta_{1}}\sin{\theta_{2}} \right ) \right ]\\ &=r_{1}r_{2}\left [ \cos{\left (\theta_{1}+\theta_{2} \right )}+i\sin{\left (\theta_{1}+\theta_{2} \right )} \right ] \end{align*} $$ 即 $$ r_{1}\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right )\cdot r_{2}\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right )=r_{1}r_{2}\left [ \cos{\left (\theta_{1}+\theta_{2} \right )}+i\sin{\left (\theta_{1}+\theta_{2} \right )} \right ] $$ 这就是说,两个复数相乘,积的模等于各复数的模的积,积的辐角等于各复数的辐角之和。
据此,两个复数$z_{1},z_{2}$相乘时,可以先画出分别与$z_{1},z_{2}$对应的向量$\overrightarrow{OP_{1}},\overrightarrow{OP_{2}}$,然后把向量$\overrightarrow{OP_{1}}$按逆时针方向旋转一个角度$\theta_{2}$(如果$\theta < 0$,就要把$\overrightarrow{OP_{1}}$按顺时针方向旋转一个角度 $\left | \theta_{2} \right |$ ),在把它的模变为原来的$r_{2}$倍,所得的向量$\overrightarrow{OP}$,就表示积$z_{1}\cdot z_{2}$(图 10)。这就是复数乘法的几何意义。
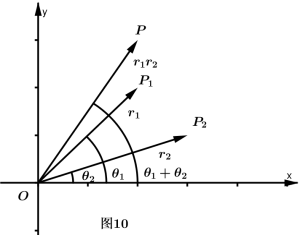
复数乘法的几何意义
用数学归纳法容易证明(读者自己证明),上面的结论可以推广到$n$个复数相乘的情况,就是:
$$ \begin{align*} z_{1}\cdot z_{2}\cdot\cdots\cdot z_{n} &=r_{1}\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right )\cdot r_{2}\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right )\cdot\cdots\cdot r_{n}\left ( \cos{\theta_{n}}+i\sin{\theta_{n}} \right )\\ &=r_{1}r_{2}\cdots r_{n}\left [ \cos{\left ( \theta_{1}+\theta_{2}+\cdots +\theta_{n} \right )} + i\sin{\left ( \theta_{1}+\theta_{2}+\cdots +\theta_{n} \right )}\right ] \end{align*} $$
因此,如果 $$ r_{1}=r_{2}=\cdots=r_{n}=r,\theta_{1}=\theta_{2}=\cdots=\theta_{n}=\theta $$ 时,就有 $$ \left [ r\left ( \cos{\theta}+i\sin{\theta} \right )^n \right ]=r^{n}\left ( \cos{n\theta}+i\sin{n\theta} \right )\left ( n\in\mathbf{N} \right ) $$
这就是说,复数的$n\left(n\in\mathbf{N}\right)$次幂的模等于这个复数的模的$n$次幂,它的辐角等于这个复数的辐角的$n$倍。这个定理叫做棣莫佛2定理。
例1:计算$\sqrt{2}\left ( \cos{\frac{\pi}{12}}+i\sin{\frac{\pi}{12}} \right )\cdot\sqrt{3}\left ( \cos{\frac{\pi}{6}}+i\sin{\frac{\pi}{6}} \right )$。
解:$\sqrt{2}\left ( \cos{\frac{\pi}{12}}+i\sin{\frac{\pi}{12}} \right )\cdot\sqrt{3}\left ( \cos{\frac{\pi}{6}}+i\sin{\frac{\pi}{6}} \right )\ =\sqrt{6}\left [ \cos\left ( \frac{\pi}{12}+\frac{\pi}{6} \right )+i\sin\left ( \frac{\pi}{12}+\frac{\pi}{6} \right ) \right ]\ =\sqrt{6}\left ( \cos{\frac{\pi}{4}}+i\sin{\frac{\pi}{4}} \right )\ =\sqrt{6}\left ( \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i \right )\ =\sqrt{3}+\sqrt{3}i$。
例2:计算$\left ( \sqrt{3}-i \right )^{6}$。
解:因为$\sqrt{3}-i=2\left ( \cos{\frac{11\pi}{6}}+i\sin{\frac{11\pi}{6}} \right )$,所以$\left (\sqrt{3}-i \right )^{6}\ =\left [2\left ( \cos{\frac{11\pi}{6}}+i\sin{\frac{11\pi}{6}} \right ) \right ]^{6}\ =2^{6}\left ( \cos{11\pi}+i\sin{11\pi} \right )\ =64\left ( \cos{\pi}+i\sin{\pi} \right )\ =64\cdot\left ( -1 \right )=-64$。
例3:如图11,向量$\overrightarrow{OZ}$与复数$-1+i$对应,把$\overrightarrow{OZ}$按逆时针方向旋转$120^\circ$,得到$\overrightarrow{OZ‘}$。求与向量$\overrightarrow{OZ’}$对应的复数(用代数形式表示)。
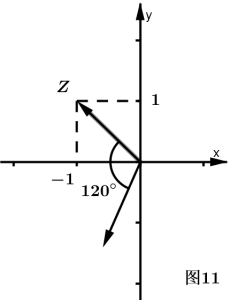
复数的旋转
解:所求的复数就是$-1+i$乘以一个复数$z_{0}$的积,这个复数$z_{0}$的模是$1$,辐角的主值是$120^\circ$。
所以所求的复数是$(-1+i)\cdot 1\left ( \cos{120^\circ}+i\sin{120^\circ} \right )\ =(-1+i)\left ( -\frac{1}{2}+\frac{\sqrt{3}}{2}i \right )\ =\frac{1-\sqrt{3}}{2}-\frac{1+\sqrt{3}}{2}i$
例4:如图 12,已知平面内并列的三个相等的正方形,利用复数证明
$\angle 1+\angle 2+\angle 3=\frac{\pi}{2}.$

例 4 图例
证明:如图建立坐标系(确定复平面),由于平行线的内错角相等,$\angle 1,\angle 2,\angle 3$分别等于复数$1+i,2+i,3+i$的辐角的主值,这样$\angle 1+\angle 2+\angle 3$就是积$\left ( 1+i \right )\left ( 2+i \right )\left ( 3+i \right )$的辐角,而 $$ \left ( 1+i \right )\left ( 2+i \right )\left ( 3+i \right )=10i $$ 其辐角的主值是$\frac{\pi}{2}$,并且$\angle 1,\angle 2,\angle 3$都是锐角,于是 $$ 0<\angle 1+\angle 2+\angle 3<\frac{3\pi}{2} $$ 所以 $$ \angle 1+\angle 2+\angle 3=\frac{\pi}{2} $$
3.2.2 除法
设$z_{1}=r_{1}\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right ),z_{2}=r_{2}\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right )$,且$z_{2}\neq 0$。因为 $$ r_{2}\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right )\cdot \frac{r_{1}}{r_{2}}\left [ \cos{\left (\theta_{1}-\theta_{2} \right )}+i\sin{\left (\theta_{1}-\theta_{2} \right )} \right ]=r_{1}\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right ) $$ 所以根据复数的除法的定义,有 $$ \frac{r_{1}\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right )}{r_{2}\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right )}=\frac{r_{1}}{r_{2}}\left [ \cos{\left (\theta_{1}-\theta_{2} \right )}+i\sin{\left (\theta_{1}-\theta_{2} \right )} \right ] $$
这就是说,两个复数相除,商的模等于被除数的模除以除数的模所得的商,商的辐角等于被除数的辐角减去除数的辐角所得的差。
例5:计算$4\left ( \cos{\frac{4\pi}{3}}+i\sin{\frac{4\pi}{3}} \right )\div 2\left ( \cos{\frac{5\pi}{6}}+i\sin{\frac{5\pi}{6}} \right )$。
解:$4\left ( \cos{\frac{4\pi}{3}}+i\sin{\frac{4\pi}{3}} \right )\div 2\left ( \cos{\frac{5\pi}{6}}+i\sin{\frac{5\pi}{6}} \right )\ =\frac{4\left ( \cos{\frac{4\pi}{3}}+i\sin{\frac{4\pi}{3}} \right )}{2\left ( \cos{\frac{5\pi}{6}}+i\sin{\frac{5\pi}{6}} \right )}\ =2\left [ \cos{\left ( \frac{4\pi}{3}-\frac{5\pi}{6} \right )}+i\sin{\left ( \frac{4\pi}{3}-\frac{5\pi}{6} \right )} \right ]\ =2\left [ \cos{\frac{\pi}{2}}+i\sin{\frac{\pi}{2}} \right ]=2\left ( 0+i \right )=2i$。
3.2.3 开方
设$\rho \left ( \cos{\phi}+i\sin{\phi} \right )$是复数$r\left ( \cos{\theta}+i\sin{\theta} \right )$的$n\left ( n\in\mathbf{N} \right )$次方根,那么 $$ r\left ( \cos{\theta}+i\sin{\theta} \right )=\left [ \rho \left ( \cos{\phi}+i\sin{\phi} \right ) \right ]^{n}=\rho^{n} \left ( \cos{n\phi}+i\sin{n\phi} \right ) $$
因为相等的复数,它们的模相等,辐角可以相差$2\pi$的整数倍,所以 $$ \begin{cases} \rho^{n}=r\\ n\phi=\theta+2k\pi\left ( k\in\mathbf{Z} \right ) \end{cases} $$ 由此可知,$$ \rho=\sqrt[n]{r},\phi=\frac{\theta+2k\pi}{n} $$ 因此$r\left ( \cos{\theta}+i\sin{\theta} \right )$的$n$次方根是 $$ \sqrt[n]{r}\left ( \cos{\frac{\theta+2k\pi}{n}} +i\sin{\frac{\theta+2k\pi}{n}}\right ) $$
当$k$取$0,1,\cdots,n-1$各值时,就可以得到上式的$n$个值。由于正弦、余弦函数的周期都是$2\pi$,当$k$取$n,n+1$以及其他各个整数值时,又重复出现$k$取$0,1,\cdots,n-1$时的结果。所以复数$r\left ( \cos{\theta}+i\sin{\theta} \right )$的$n$次方根3是 $$ \sqrt[n]{r}\left ( \cos{\frac{\theta+2k\pi}{n}} +i\sin{\frac{\theta+2k\pi}{n}}\right )\left ( k=0,1,\cdots,n-1 \right ) $$
这就是说,复数的$n\left ( n\in\mathbf{N} \right )$次方根是$n$个复数,它们的模都等于这个复数的模的$n$次算术根,它们的辐角分别等于这个复数的辐角与$2\pi$的$0,1,\cdots,n-1$倍的和的$n$分之一。
例6:求$1-i$的立方根。
解:因为 $$ 1-i=\sqrt{2}\left ( \cos{\frac{7\pi}{4}}+i\sin{\frac{7\pi}{4}} \right ) $$ 所以$1-i$的立方根是 $$ \sqrt[6]{2}\left ( \cos{\frac{\frac{7\pi}{4}+2k\pi}{3}}+i\sin{\frac{\frac{7\pi}{4}+2k\pi}{3}} \right )=\sqrt[6]{2}\left ( \cos{\frac{7\pi+8k\pi}{12}}+i\sin{\frac{7\pi+8k\pi}{12}} \right )\left ( k=0,1,2 \right ] $$ 即$1-i$的立方根是下面三个复数:$$ \sqrt[6]{2}\left ( \cos{\frac{7\pi}{12}}+i\sin{\frac{7\pi}{12}} \right ) $$ $$ \sqrt[6]{2}\left ( \cos{\frac{5\pi}{4}}+i\sin{\frac{5\pi}{4}} \right ) $$ $$ \sqrt[6]{2}\left ( \cos{\frac{23\pi}{12}}+i\sin{\frac{23\pi}{12}} \right ) $$
例7:设$a\in\mathbf{R^{+}}$,求$-a$的平方根。
解:因为$-a=a\left(\cos{\pi}+i\sin{\pi}\right)$,所以$-a$的平方根是 $$ \sqrt{a}\left ( \cos{\frac{\pi+2k\pi}{2}}+i\sin{\frac{\pi+2k\pi}{2}} \right )\left ( k=0,1 \right ) $$ 即$-a$的平方根是下面两个复数:$$ \sqrt{a}\left ( \cos{\frac{\pi}{2}}+i\sin{\frac{\pi}{2}} \right ),\sqrt{a}\left ( \cos{\frac{3\pi}{2}}+i\sin{\frac{3\pi}{2}} \right ) $$ 或 $$ \sqrt{a}i,-\sqrt{a}i $$
从例7可以看到,$a\in\mathbf{R^{+}}$时,$-a$的平方根是$\pm\sqrt{a}i$。
我们知道,对于实系数一元二次方程$ax^{2}+bx+c=0$,如果$b^{2}-4ac< 0$,那么它在实数集$\mathbf{R}$中没有根。现在我们在复数集$\mathbf{C}$中考察这种情况。经过变形,原方程可化为 $$ x^{2}+\frac{b}{a}x=-\frac{c}{a} $$ 所以 $$ x^{2}+2\cdot x\cdot \frac{b}{2a}+\left ( \frac{b}{2a} \right )^{2}=\left ( \frac{b}{2a} \right )^{2}-\frac{c}{a} $$ 进一步化简得 $$ \left ( x+\frac{b}{2a} \right )^{2}=\frac{b^{2}-4ac}{\left ( 2a \right )^2} $$ 即 $$ \left ( x+\frac{b}{2a} \right )^{2}=-\left [ \frac{-\left ( b^{2}-4ac \right )}{\left ( 2a \right )^2} \right ] $$
由于$\frac{-\left ( b^{2}-4ac \right )}{\left ( 2a \right )^2}\in\mathbf{R^{+}}$,根据例 7,我们得到 $$ x+\frac{b}{2a}=\frac{\pm\sqrt{\left ( b^{2}-4ac \right )}i}{2a} $$ 所以方程$ax^{2}+bx+c=0$在复数集$\mathbf{C}$中有两个根 $$ x=\frac{-b\pm\sqrt{-\left ( b^{2}-4ac \right )}i}{2a}\left ( b^{2}-4ac< 0 \right ) $$ 显然,它们是一对共轭复数。
例8:在复数集$\mathbf{C}$中解方程$x^{2}-4x+5=0$。
解:因为$b^{2}-4ac=16-20=-4< 0$,所以$x=\frac{4\pm 2i}{2}=2\pm i$。
根据以前学过的一元二次方程的有关知识,我们知道,例8中方程左边的二次三项式$x^2-4x+5$在复数集$\mathbf{C}$中就可以通过求根的方法分解成两个一次因式的积,即 $$ x^{2}-4x+5=\left [ x-\left ( 2+i \right ) \right ]\left [ x-\left ( 2-i \right ) \right ]=\left ( x-2-i \right )\left ( x-2+i \right ) $$ 形如$a_{n}x^{n}+a_{0}=0$($a_{0},a_{n}\in\mathbf{C}$,且$a_{n}\neq 0$)的方程叫做二项方程。任何一个二项方程都可以化成$x^{n}=b\left(b\in\mathbf{C}\right)$的形式,因此,都可以通过复数开方来求根。
例9:在复数集$C$中解方程$x^{5}=32$。
解:原方程就是 $$ x^{5}=32\left ( \cos{0}+i\sin{0} \right ) $$ 所以 $$ x=\sqrt[5]{32}\left ( \cos{\frac{0+2k\pi}{5}}+i\sin{\frac{0+2k\pi}{5}} \right )\ =2\left [ \cos{\left ( k\cdot\frac{2\pi}{5} \right )}+i\sin{\left ( k\cdot\frac{2\pi}{5} \right )} \right ]\left ( k=0,1,2,3,4 \right ) $$ 就是 $$ x_{1}=2\left ( \cos{0}+i\sin{0} \right )=2 $$ $$ x_{2}=2\left ( \cos{\frac{2\pi}{5}}+i\sin{\frac{2\pi}{5}} \right ) $$ $$ x_{3}=2\left ( \cos{\frac{4\pi}{5}}+i\sin{\frac{4\pi}{5}} \right ) $$ $$ x_{4}=2\left ( \cos{\frac{6\pi}{5}}+i\sin{\frac{6\pi}{5}} \right ) $$ $$ x_{5}=2\left ( \cos{\frac{8\pi}{5}}+i\sin{\frac{8\pi}{5}} \right ) $$
这个方程的根的几何意义是复平面内的五个点,这些点均匀分布在以原点为圆心,以$2$为半径的圆上(圆13)。
一般地,方程$x^{n}=b\left(b\in\mathbf{C}\right)$的根的几何意义是复平面内的$n$个点,这些点均匀分布在以原点为圆心,以 $\sqrt[n]{\left | b \right |}$ 为半径的圆上。

复数根式的几何意义
*四、复数的指数形式
在科学技术,特别实在电工和无线电计算中,为了方便起见,还采用复数的另一种表示——复数的指数形式。
我们把模为$1$,辐角为$\theta$(以弧度为单位)的复数 $$ \cos{\theta}+i\sin{\theta} $$ 用记号$e^{i\theta}$来表示,即4 $$ e^{i\theta}=\cos{\theta}+i\sin{\theta} $$ 例如, $$ e^{i\frac{\pi}{2}}=\cos{\frac{\pi}{1}+i\sin{\frac{\pi}{1}}}=i $$ $$ e^{i\frac{\pi}{3}}=\cos{\frac{\pi}{3}+i\sin{\frac{\pi}{3}}}=\frac{1}{2}+\frac{\sqrt{3}}{2}i $$ 又如,$$ \cos{\frac{5\pi}{6}}+i\sin{\frac{5\pi}{6}} $$ 可以写成 $$ e^{i\frac{5\pi}{6}} $$ $$ \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i=\cos{\frac{\pi}{4}}+i\sin{\frac{\pi}{4}} $$ 可以写成 $$ e^{i\frac{\theta}{4}} $$
引入记号$e^{i\theta}=\cos{\theta}+i\sin{\theta}$之后,任何一个复数 $$ z=r\left(\cos{\theta}+i\sin{\theta}\right) $$ 就可以表示成 $$ z=re^{i\theta} $$ 的形式。我们把这一表达式叫做复数的指数形式。
根据复数的指数形式的定义,我们有 $$ e^{i\theta_{1}}\cdot e^{i\theta_{2}}\ =\left ( \cos{\theta_{1}}+i\sin{\theta_{1}} \right )\left ( \cos{\theta_{2}}+i\sin{\theta_{2}} \right )\ =\cos{\left ( \theta_{1}+\theta_{2} \right )}+i\sin{\left ( \theta_{1}+\theta_{2} \right )}\ =e^{i\left ( \theta_{1}+\theta_{2} \right )} $$ 即 $$ e^{i\theta_{1}}\cdot e^{i\theta_{2}}=e^{i\left ( \theta_{1}+\theta_{2} \right )} $$
同样可证 $$ \left ( e^{i\theta} \right )^{n}=e^{in\theta}\left ( n\in\mathbf{N} \right ) $$ $$ \frac{e^{i\theta_1}}{e^{i\theta_{2}}}=e^{i\left ( \theta_{1}-\theta_{2} \right )} $$ 上述性质与我们过去学过的实数指数幂的性质一致,所以把复数从三角形式改写成指数形式后,可以运用实数集$\mathbf{R}$中的幂运算律(注意:乘方的指数限于自然数)来进行运算。这里我们仿照实数集$\mathbf{R}$中的说法,把$e^{i\theta}$叫做以$e$为底、$i\theta$为指数的幂。
对于开方运算,复数$re^{i\theta}$的$n\left(n\in\mathbf{N}\right)$次方根是 $$ \sqrt[n]{r}e^{i\frac{\theta+2k\pi}{n}}\left ( k=0,1,\cdots,n-1 \right ) $$
例1:把复数$z=2i$表示成指数形式。
解:$z=2i=2\left ( \cos{\frac{\pi}{1}}+i\sin{\frac{\pi}{2}} \right )=2e^{i\frac{\pi}{2}}$。
例2:把$\sqrt{2}e^{-i\frac{\pi}{4}},\sqrt{5}e^{i\frac{2\pi}{3}}$表示成三角形式及代数形式。
解: $$ \sqrt{2}e^{-i\frac{\pi}{4}}=\sqrt{2}\left [ \cos\left ( -\frac{\pi}{4} \right )+i\sin{\frac{\pi}{4}} \right ]=1-i $$ $$ \sqrt{5}e^{i\frac{2\pi}{3}}=\sqrt{5}\left [ \cos\left ( -\frac{2\pi}{3} \right )+i\sin{\frac{2\pi}{3}} \right ]=-\frac{\sqrt{5}}{2}+\frac{\sqrt{15}}{2}i $$
例3:用$e^{i\theta}$与$e^{-i\theta}$表示$\cos{\theta}$与$\sin{\theta}$。
解:因为 $$ e^{i\theta}=\cos{\theta}+i\sin{\theta} $$ $$ e^{-i\theta}=\cos{\left ( -\theta \right )}+i\sin\left ( -\theta \right )=\cos{\theta}-i\sin{\theta} $$ 因此 $$ \cos{\theta}=\frac{e^{i\theta}+e^{-i\theta}}{2},\quad \sin{\theta}=\frac{e^{i\theta}-e^{-i\theta}}{2i} $$