距离的定义
在机器学习中,我们通过计算不同样本在特征空间中的距离来评估样本间的相似度,进而为其进行分类。根据样本特征空间的不同,我们需要选择合适的距离度量方法。一般而言,对于距离度量函数$d(x,y)$,其需要满足如下性质:
- 非负性:$d(x,y)\geq 0$
- 同一性:$d(x,y)=0\Leftrightarrow x=y$
- 对称性:$d(x,y)=d(y,x)$
- 三角不等式:$d(x,y)\leq d(x,z)+d(z,y)$
根据样本特征空间的不同,我们把度量的距离分为:空间距离、字符距离、集合距离、分布距离。
空间距离
欧几里得距离(Euclidean Distance)
欧几里得距离用于描述欧式空间中任意两点间的直线距离,常被称作欧几里得范数,或$\mathcal{L}_2$范数。对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的欧几里得距离定义为:
$$d=\sqrt{\sum_{i=1}^{n}{\left(x_i-y_i\right)^2}}$$
在 Python 中用于计算任意两点间欧几里得距离的代码如下:
| |
曼哈顿距离(Manhattan Distance)
曼哈顿距离用于描述标准坐标系中任意两点间的绝对轴距之和,常被称作曼哈顿范数,或$\mathcal{L}_1$范数。对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的曼哈顿距离定义为:
$$d=\sqrt{\sum_{i=1}^{n}{\left|x_i-y_i\right|}}$$
下图所示红色路径为曼哈顿距离,绿色路径为欧几里得距离,蓝色路径和黄色路径为等价曼哈顿距离。曼哈顿距离的发明是为了应对早期计算图形学领域中浮点运算代价高的情况,采用曼哈顿距离代替欧几里得距离进行图形渲染。
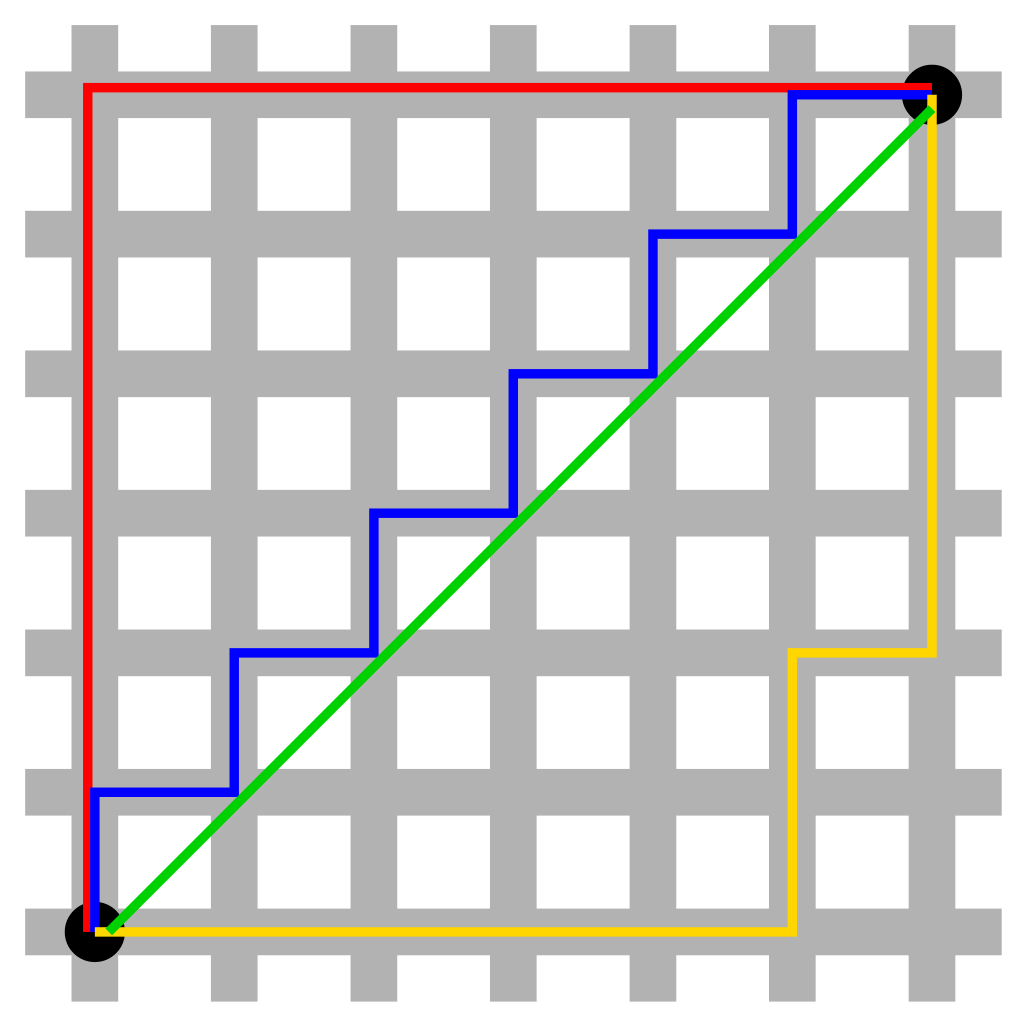
曼哈顿距离(Manhattan Distance)
在 Python 中用于计算任意两点间曼哈顿距离的代码如下:
| |
切比雪夫距离(Chebyschev Distance)
切比雪夫距离用于描述标准坐标系中任意两点间的绝对轴距最大值,常被称作切比雪夫范数,或$\mathcal{L}_\infty$范数。对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的切比雪夫距离定义为:
$$d=\max\left|x_i-y_i\right|$$
以下图所示位于 F6 的“王”为例,其到棋盘上任意一点的切比雪夫距离即为它需要移动的步数。需要注意的是,在国际象棋中“王”每次可以朝任意方向移动一格。

切比雪夫距离(Chebyschev Distance)
在 Python 中用于计算任意两点间切比雪夫距离的代码如下:
| |
闵可夫斯基距离(Minkowski Distance)
闵可夫斯基距离并非一种新型的距离度量方式,而是一种对于多种不同距离度量的概括性表述。对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的闵可夫斯基距离定义为:
$$d=\left(\sum_{i=1}^{n}{\left|x_i-y_i\right|^p}\right)^{1/p}$$
其中,$p$为闵可夫斯基距离参数。当$p=1$时,闵可夫斯基距离退化为曼哈顿距离;当$p=2$时,闵可夫斯基距离退化为欧几里得距离;当$p\rightarrow\infty$时,闵可夫斯基距离退化为切比雪夫距离,如下图所示:
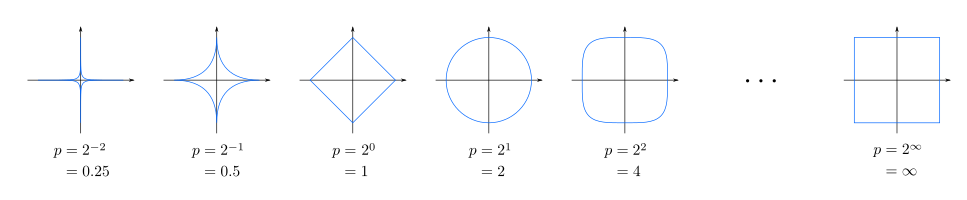
闵可夫斯基距离(Minkowski Distance)
在 Python 中用于计算任意两点间闵可夫斯基距离的代码如下:
| |
标准化欧几里得距离(Standardized Euclidean Distance)
标准化欧几里得距离是将欧式空间中任意两点的分量都“标准化”到均值、方差一致的区间,记每个分量的均值为$\mu$,方差为$\sigma_i^2$,“标准化”结果为$X^*$:
$$X^*=\frac{X-\mu}{\sigma^2}$$
对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的标准化欧几里得距离定义为:
$$d=\sqrt{\sum_{i=1}^{n}{\left(\frac{x_i-y_i}{\sigma_i^2}\right)^2}}$$
如果将$1/\sigma^2$看做权重,则标准化欧几里得距离可以被认为是加权欧几里得距离。
在 Python 中用于计算任意两点间标准化欧几里得距离的代码如下(需要注意 sigma ≠ 0):
| |
马氏距离(Mahalanobis Distance)
马氏距离由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出,用于表示数据的协方差距离,它可以有效地表示两个未知样本集之间的相似度。对于$n$维空间中的任意两个样本集$\textbf{X}$和$\textbf{Y}$的马氏距离定义为:
$$d=\sqrt{\left(\textbf{X}-\textbf{Y}\right)^T\Sigma^{-1}\left(\textbf{X}-\textbf{Y}\right)}$$
其中,$\Sigma$为样本集$X$和$Y$的协方差矩阵。若协方差矩阵为单位矩阵,则马氏距离退化为欧几里得距离;若协方差矩阵为对角矩阵,则马氏距离退化为标准化欧几里得距离。
需要注意的是,马氏距离的计算需要确保$\Sigma$的逆矩阵存在,否则可以直接采用欧几里得距离进行计算。此外,马氏距离不受量纲的影响,它可以排除变量之间相关性的干扰,但同时也夸大了微小变化量的作用。例如,若将两个相同的样本放入两个不同的总体中,经计算的到的马氏距离也是不同的(除非它们的$\Sigma$恰巧相同)。
在 Python 中用于计算任意两个样本集间马氏距离的代码如下:
| |
兰氏距离(Lance and Williams Distance)
兰氏距离又被称为堪培拉距离(Canberra Distance),可以理解为加权曼哈顿距离。对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的兰氏距离定义为:
$$d=\sum_{i=1}^{n}{\frac{\left|x_i-y_i\right|}{\left|x_i\right|+\left|y_i\right|}}$$
在 Python 中用于计算任意两点间兰氏距离的代码如下:
| |
余弦相似度(Cosine Similarity)
在几何学中,通常采用余弦相似度来度量两个向量间的夹角,其取值为$[-1,1]$。对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的余弦相似度定义为:
$$\cos{\left(\vec{x},\vec{y}\right)}=\frac{\vec{x}\cdot\vec{y}}{\left|\vec{x}\right|\cdot\left|\vec{y}\right|}=\frac{\displaystyle\sum_{i=1}^{n}{x_i\cdot y_i}}{\sqrt{\displaystyle\sum_{i=1}^{n}{x_i^2}}\cdot\sqrt{\displaystyle\sum_{i=1}^{n}{y_i^2}}}$$
当$\cos{\left(\vec{x},\vec{y}\right)}\rightarrow0$时,两向量完全正交;当$\cos{\left(\vec{x},\vec{y}\right)}\rightarrow1$时,两向量完全重合;当$\cos{\left(\vec{x},\vec{y}\right)}\rightarrow -1$时,两向量完全相反。在 Python 中用于计算任意两点间余弦相似度的代码如下:
| |
测地距离(Geodesic Distance)
测地距离原指球体表面上两点间的最短距离,后来被推广到其它领域。在图论中,测地距离为两顶点间的最短路径;在欧式空间中,测地距离为欧几里得距离;在非欧空间中,测地距离为连接两点间的最短圆弧。如下图所示:
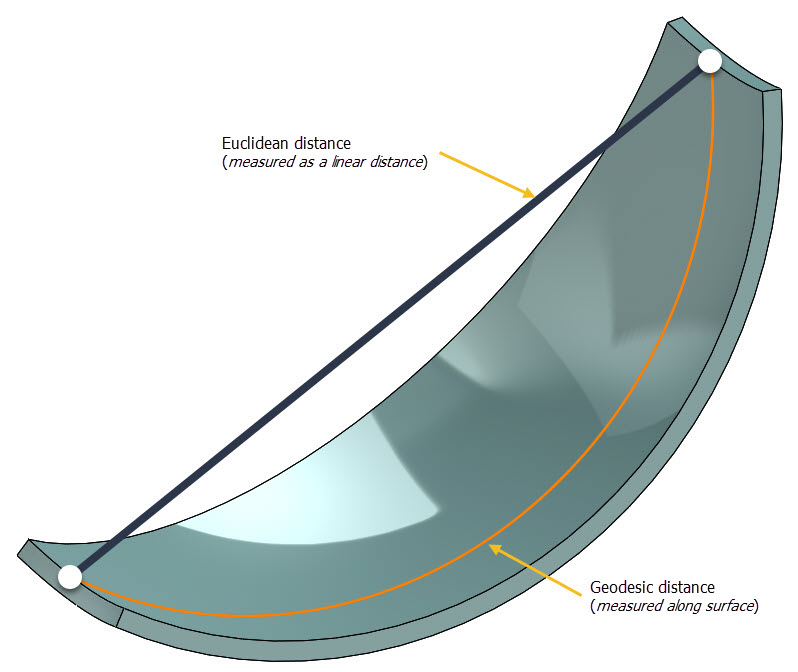
测地距离(Geodesic Distance)
布雷柯蒂斯距离(Bray Curtis Distance)
布雷柯蒂斯距离主要用于生态学和环境科学领域,用于计算不同样本间的差异。对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的布雷柯蒂斯距离定义为:
$$d=\frac{\displaystyle \sum_{i=1}^{n}{\left|x_i-y_i\right|}}{\displaystyle \sum_{i=1}^{n}{x_i}+\sum_{i=1}^{n}{y_i}}$$
在 Python 中用于计算任意两点间布雷柯蒂斯距离的代码如下:
| |
半正矢距离(Haversine Distance)
半正矢距离用于计算任意两经纬点间的距离,对于空间中的任意两经纬点$A(\mathrm{lon}_1,\mathrm{lat}_1)$和$B(\mathrm{lon}_2,\mathrm{lat}_2)$的半正矢距离定义为:
$$d=2r\cdot\arcsin{\sqrt{\sin^2{\frac{\mathrm{lat}_2-\mathrm{lat}_1}{2}}+\cos{(\mathrm{lat}_1)}\cos{(\mathrm{lat}_2)}\sin^2{\frac{\mathrm{lon}_2-\mathrm{lon}_1}{2}}}}$$
其中,$r$为半径。在 Python 中用于计算任意两经纬点间半正矢距离的代码如下:
| |
字符距离
汉明距离(Hamming Distance)
汉明距离由两个字符串对应位不同的数量决定,通常用于数据传输差错控制编码领域。对于长度为$n$的任意两个字符串$A=x_1x_2\cdots x_n$和$B=y_1y_2\cdots y_n$的汉明距离定义为:
$$d=\sum_{i=0}^{n}{x_i\otimes y_i}$$
汉明距离也可以理解为将$A$变为$B$的最小操作次数。在 Python 中用于计算任意两个字符串间汉明距离的代码如下:
| |
莱文斯坦距离(Levenshtein Distance)
莱文斯坦距离又被称为编辑距离(Edit Distance),用于度量两个字符串之间的差异,定义为:将字符串$A$转化为字符串$B$所需的最少单字符编辑(插入、删除或替换)次数。对于长度为$n$的任意两个字符串$A=x_1x_2\cdots x_n$和$B=y_1y_2\cdots y_n$,$A$的前$i$个字符和$B$的前$j$个字符的莱文斯坦距离定义为:
$$d(i,j) = \begin{align*} \left{\begin{matrix} \max{\left(i,j\right)}, & \min{\left(i,j\right)}=0 \ \min{\left[d(i-1,j),d(i,j-1), d(i,j)\right]} + I(i,j), & \min{\left(i,j\right)\neq 0} \end{matrix}\right. \end{align*}$$
其中,$I(\cdot)$为指示函数,当$x_i=y_j$时,$I(i,j)=0$;当$x_i\neq y_j$时,$I(i,j)=1$。在 Python 中用于计算任意两个字符串间莱文斯坦距离的代码如下:
| |
归一化 Google 距离(Normalized Google Distance)
归一化 Google 距离是由给定一组关键词集合的 Google 搜索引擎所返回的命中数量决定的,它是一种语义相似度量方法。对于长度为$n$的任意两个字符串$A=x_1x_2\cdots x_n$和$B=y_1y_2\cdots y_n$的归一化 Google 距离定义为:
$$d=\frac{\max{\left[\log{f(A)},\log{f(B)}\right]}-\log{f(A,B)}}{\log{M}-\min{\left[\log{f(A)}, \log{f(B)}\right]}}$$
其中,$M$为 Google 搜索引擎所返回的网页总数;$f(x)$和$f(y)$分别为 Google 搜索引擎返回关于字符串$A$和字符串$B$的命中数量;$f(A,B)$为 Google 搜索引擎返回关于字符串$A$和字符串$B$同时出现的命中数量。
Jaro-Winkler 相似度(Jaro-Winkler Similarity)
Jaro 相似度用于评估两个字符串间的相似度,对于长度为$n$的任意两个字符串$A=x_1x_2\cdots x_n$和$B=y_1y_2\cdots y_n$的 Jaro 相似度定义为:
$$d_j=\frac{1}{3}\cdot\left(\frac{m}{|A|}+\frac{m}{|B|}+\frac{m-t}{m}\right)$$
其中,$m$是匹配的字符数,$t$是替换的字符数。
Jaro-Winkler 相似度在 Jaro 相似度的基础上引入了前缀的概念,对于长度为$n$的任意两个字符串$A=x_1x_2\cdots x_n$和$B=y_1y_2\cdots y_n$的 Jaro-Winkler 相似度定义为:
$$d_w=d_j+l\cdot p\cdot(1-d_j)$$
其中,$l$为字符串$A$和字符串$B$的共同前缀的字符数;$p$为缩放因子(常取$p=0.1$)。
李距离(Lee Distance)
李距离是编码理论中用于描述字符串距离的方案,对于使用包含$q$个字母的字母表且长度为$n$的任意两个字符串$A=x_1x_2\cdots x_n$和$B=y_1y_2\cdots y_n$的李距离定义为:
$$d=\sum_{i=0}^{n}{\min{\left(\left|x_i-y_i\right|,q-\left|x_i-y_i\right|\right)}}$$
当$q=2$或$q=3$时,李距离退化为汉明距离。
集合距离
杰卡德相似系数(Jaccard Similarity Coefficient)
杰卡德相似系数是指两个集合$A$和$B$中相同元素在所有元素中的占比,定义为$J(A,B)$:
$$J(A,B)=\frac{\left|A\cap B\right|}{\left|A\cup B\right|}$$
杰卡德距离(Jaccard Distance)是指两个集合$A$和$B$中不同元素在所有元素中的占比,定义为$J_\delta(A,B)$:
$$J_\delta(A,B)=1-J(A,B)=1-\frac{\left|A\cap B\right|}{\left|A\cup B\right|}$$
在 Python 中用于计算任意两个集合间杰卡德相似系数的代码如下:
| |
奥奇亚系数(Ochiia Coefficient)
奥奇亚系数是指两个集合$A$和$B$中相同元素与两集合大小几何平均值的比值,定义为$K(A,B)$:
$$K(A,B)=\frac{\left|A\cap B\right|}{\sqrt{\left|A\right|\times\left|B\right|}}$$
戴斯系数(Dice Coefficient)
戴斯系数除了可以用来衡量两个集合间的距离,还可以用来衡量两个字符串间的距离,定义为$D(A,B)$:
$$D(A,B)=\frac{2\left|A\cap B\right|}{\left|A\right|+\left|B\right|}$$
豪斯多夫距离(Hausdorff Distance)
豪斯多夫距离用于度量两个集合$A$和$B$间的距离,定义为$H(A,B)$:
$$H(A,B)=\max{\left[h(A,B),h(B,A)\right]}$$
其中,$h(\cdot)$为双向豪斯多夫距离,定义为:
$$h(A,B)=\max_{a\in A}{\min_{b\in B}{\left |a-b\right|}}$$
其中,$h(A,B)$为从集合$A$到集合$B$的单向豪斯多夫距离,$h(B,A)$为从集合$B$到集合$A$的单向豪斯多夫距离。
分布距离
皮尔逊相关系数(Pearson Correlation Coefficient)
皮尔逊相关系数又被称为皮尔逊积矩相关技术(Pearson Product Moment Correlation Coefficient,PPMCC/PCC),用于度量两个变量$X$和$Y$之间的线性相关性。与上文提到的余弦相似度不同,皮尔逊相关系数不受平移变换的影响。对于$n$维空间中的任意两个分布$X$和$Y$的皮尔逊相关系数定义为:
$$\rho(X,Y)=\frac{\mathrm{cov}(X,Y)}{\sigma(X)\cdot\sigma(Y)}=\frac{\mathrm{E}\left[\left(X-X_\mu\right)\left(Y-Y_\mu\right)\right]}{\sigma(X)\cdot\sigma(Y)}$$
皮尔逊相关系数与余弦相似度的关系为:
$$\rho(X,Y)=\frac{\mathrm{E}\left[\left(X-X_\mu\right)\left(Y-Y_\mu\right)\right]}{\sigma(X)\cdot\sigma(Y)}=\frac{\displaystyle\sum_{i=1}^{n}{\left(X-X_\mu\right)\cdot\left(Y-Y_\mu\right)}}{\left|X-X_\mu\right|\cdot\left|Y-Y_\mu\right|}=\cos{\left(X-X_\mu,Y-Y_\mu\right)}$$
在 Python 中用于计算任意两个分布间皮尔逊相关系数的代码如下:
| |
卡方度量(Chi-square Measure)
$\mathcal{X}^2$检验通常用于检验某一观测分布是否符合典型理论分布。若观测频数与期望频数差异越小,则$\mathcal{X}^2$值越小;若观测频数与期望频数差异越大,则$\mathcal{X}^2$值越大。因此,$\mathcal{X}^2$值可以用于描述观测分布与理论分布的差异。对于$n$维空间中的任意两个分布$X$和$Y$的$\mathcal{X}^2$统计量定义为:
$$\mathcal{X}^2=\sum_{i=1}^{n}{\frac{\left(x_i-y_i\right)^2}{y_i}}=\sum_{i=1}^{k}{\frac{\left(x_i-n\cdot p_i\right)^2}{k\cdot p_i}}$$
其中,$x_i$为$X$在$i$的频数,$y_i$为$Y$在$i$的频数,$k$为总频数,$p_i$为$Y$在$i$的概率。在 Python 中用于计算任意两个分布间卡方度量的代码如下:
| |
交叉熵(Cross Entropy)
交叉熵是香农信息论中的重要概念,用于度量两个分布之间的差异信息。对于$n$维空间中的任意两个分布$X$和$Y$的交叉熵定义为:
$$H(X,Y)=-\int_{p}{X(p)\cdot Y(p)\mathrm{d}p}$$
若基于分布$X$对分布$X$进行编码,其编码长度的期望为:
$$H(X)=-\int_{p}{X(p)\mathrm{d}p}$$
若基于分布$Y$对分布$X$进行编码,其编码长度的期望即为交叉熵$H(X,Y)$。在 Python 中用于计算任意两个分布间交叉熵的代码如下:
| |
KL 散度(Kullback-Leibler Divergence)
KL 散度又被称为相对熵(Relative Entropy)或信息散度(Information Divergence),用于度量两个分布间的差异,对于$n$维空间中的任意两个分布$X$和$Y$的 KL 散度定义为:
$$\mathrm{KL}(X|Y)=\int_{p}{X(p)\cdot\log{\frac{X(p)}{Y(p)}}\mathrm{d}p}$$
若基于分布$X$对分布$X$进行编码,其编码长度的期望为:
$$H(X)=-\int_{p}{X(p)\log{X(p)}\mathrm{d}p}$$
若基于分布$Y$对分布$X$进行编码,其编码长度的期望即为交叉熵$H(X,Y)$,其多出的编码长度为:
$$\mathrm{KL}(X|Y)=H(X)-H(X,Y)$$
在 Python 中用于计算任意两个分布间 KL 散度的代码如下:
| |
JS 散度(Jensen-Shannon Divergence)
JS 散度是 KL 散度的变体,解决了 KL 散度非对称的问题,对于$n$维空间中的任意两个分布$X$和$Y$的 JS 散度定义为:
$$\mathrm{JS}(X|Y)=\frac{1}{2}\cdot\mathrm{KL}(X|\frac{X+Y}{2})+\frac{1}{2}\cdot\mathrm{KL}(Y|\frac{X+Y}{2})$$
在 Python 中用于计算任意两个分布间 JS 散度的代码如下:
| |
海林格距离(Hellinger Distance)
对于$n$维空间中的任意两个分布$X$和$Y$的海林格距离定义为:
$$d={\frac{1}{\sqrt{2}}\cdot\sqrt{\sum_{i=1}^{n}{\left(\sqrt{x_i}-\sqrt{y_i}\right)^2}}}$$
在 Python 中用于计算任意两个分布间海林格距离的代码如下:
| |
α 散度(α Divergence)
对于$n$维空间中的任意两个分布$X$和$Y$的 α 散度被定义为:
$$d=\frac{4}{1-\alpha^2}\cdot\left[1-\int_p{X(p)^{(1+\alpha)/2}\cdot Y(p)^{(1-\alpha)/2}}\mathrm{d}x\right]$$
其中,$-\infty<\alpha<+\infty$为连续参数。当$\alpha\rightarrow 1$时,α 散度退化为 KL 散度;当$\alpha\rightarrow 0$时,α 散度退化为海林格距离(仅相差常系数)。
F 散度(F Divergence)
对于$n$维空间中的任意两个分布$X$和$Y$的 F 散度被定义为:
$$\mathrm{D}(X|Y)=\int_p{Y(p)\cdot f\left[\frac{X(p)}{Y(p)}\right]\mathrm{d}p}$$
其中,函数$f(\cdot)$需满足:(1)$f(\cdot)$为凸函数;(2)$f(1)=0$。下表给出了$f(\cdot)$取不同值时,F 散度对应的结果。
| 散度 | $f(\cdot)$ |
|---|---|
| 卡方距离 | $(t-1)^2$ |
| KL 散度 | $x\log{x}$ |
| 逆 KL 散度 | $-\log{x}$ |
| 海林格距离 | $\left(\sqrt{x}-1\right)^2$ |
| α 散度 | $4/(1-\alpha)^2\cdot\left(1-x^{(1+\alpha)/2}\right)$ |
在 Python 中用于计算任意两个分布间 F 散度(海林格距离)的代码如下:
| |
布雷格曼散度(Bregman Divergence)
对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的欧几里得距离定义为:
$$d(x,y)=\sqrt{\sum_{i=1}^{n}{\left(x_i-y_i\right)^2}}$$
将上式两侧平方后,得到:
$$d^2(x,y)=\sum_{i=1}^{n}{\left(x_i-y_i\right)^2}$$
定义$<x,y>=\sum_{i=1}^{n}{x_i\cdot y_i}$,$\left|x\right|=\sqrt{<x,x>}$,上式可改写为:
$$d^2(x,y)=\sum_{i=1}^{n}{\left(x_i-y_i\right)^2}=<x-y,x-y>=\left|x\right|^2-\left(\left|y\right|^2+<2y,x-y>\right)$$
此处的距离即为欧几里得模函数和其在$x$处切线在$y$处的点估计差。推广该概念后,对于$n$维空间中的任意两点$A(x_1,x_2,\cdots,x_n)$和$B(y_1,y_2,\cdots,y_n)$的布雷格曼散度定义为:
$$d(x,y)=f(x)-\left[f(y)+<\nabla f(x),x-y >\right]$$
表给出了$f(\cdot)$取不同值时,布雷格曼散度对应的结果。
| 散度 | $f(\cdot)$ |
|---|---|
| 平方损失 | $x^2$ |
| / | $x\log{x}$ |
| Logistic 损失 | $x\log{x}+(1-x)\log{(1-x)}$ |
| Itakura-Saito 距离 | $-\log{x}$ |
| / | $e^x$ |
| 平方欧几里得距离 | $\left|x\right|^2$ |
| 马氏距离 | $\mathbf{X}^TA\mathbf{X}$ |
| KL 散度 | $\sum_{i=1}^{n}{x_i\log{x_i}}$ |
Wasserstein 距离(Wasserstein Distance)
Wasserstein 距离被称为推土机距离,用于表示两个分布的相似度。Wasserstein 距离定义为把分布$X$转变成分布$Y$所需移动的平均距离的最小值,如下图所示:
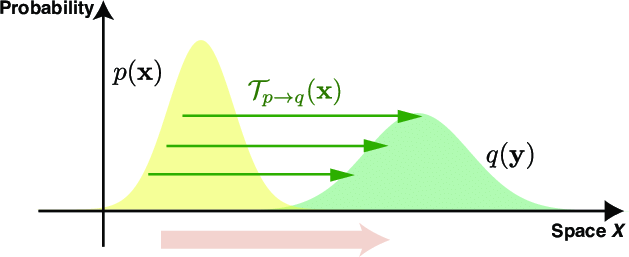
Wasserstein 距离(Wasserstein Distance)
对于$n$维空间中的任意两个分布$X$和$Y$的 Wasserstein 距离定义为:
$$d=\inf_{\gamma\sim\Pi(X,Y)}{\mathrm{E}_{p,q\sim\gamma}\left|p-q\right|}$$
其中,$\Pi(X,Y)$为分布$X$和分布$Y$构成的联合分布的集合,$\gamma$为$\Pi(X,Y)$中任意分布,$p$和$q$是分布$\gamma$中的样本。
巴氏距离(Bhattacharyya Distance)
巴氏系数可以用来度量两个分布的相似性,对于$n$维空间中的任意两个分布$X$和$Y$的巴氏系数定义为:
$$c_b=\int_{p}{\sqrt{X(p)\cdot Y(p)}\mathrm{d}p}$$
巴氏距离定义为:
$$d_b=-\ln{c_b}$$
需要注意的是,海林格距离$d=\sqrt{1-d_b}$。在 Python 中用于计算任意两个分布间巴氏距离的代码如下:
| |
最大均值差异(Maximum Mean Discrepancy)
最大均值差异是迁移学习领域中最为广泛使用的一种损失函数,它度量了再生希尔伯特空间中两个不同分布间的距离。通过在样本空间寻找连续函数$f:X\rightarrow R$随机投影后,分别求这两个分布在$f$上函数值的均值,并通过做差得到均值差异(Mean Discrepancy)。最大化均值差异即为寻找一个$f$使得均值差异最大。对于$n$维空间中的任意两个分布$X$和$Y$的最大均值差异定义为:
$$d=\sup_{|f|_\mathrm{H} \leq 1}{\mathrm{E}_p[f(X)]-\mathrm{E}_q[f(Y)]}$$
点间互信息(Pointwise Mutual Information)
点间互信息用来衡量两个分布的相关性,对于$n$维空间中的任意两个分布$X$和$Y$的点间互信息定义为:
$$d=\log{\frac{p(X,Y)}{p(X)\cdot p(Y)}}=\log{\frac{p(X|Y)}{p(X)}}=\log{\frac{p(Y|X)}{p(Y)}}$$
若$X$和$Y$不相关,则$P(X,Y)=P(X)\cdot P(Y)$。